题目内容
(2005
全国I,20)9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为0.5.若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没有发芽,则这个坑需要补种.假定每个坑至多补种一次,每次种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望(精确到0.01).
答案:略
解析:
提示:
解析:
|
解析:因为单个坑内的 3粒种子都不发芽的概率为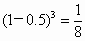 ,所以单个坑不需要补种的概率为 ,所以单个坑不需要补种的概率为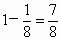 . .
3 个坑都不需要补种的概率为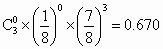 , ,
恰有 1个坑需要补种的概率为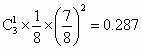 , ,
恰有 2个坑需要补种的概率为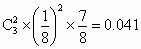 , ,
3 个坑都需要补种的概率为 . .
补种费用 ξ的分布列为
ξ 的数学期望为Eξ=0 ×0.670+10×0.287+20×0.041+30×0.002=3.75. |
提示:
|
剖析:对于每个坑内的 3粒种子相当于是独立重复试验,本问题需先求出每个坑需要补种及不需要补种的概率,从而使问题迎刃而解. |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,给出了计算
如图,给出了计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 40 |
| A、i<20°n=n+2 |
| B、i=20°n=n+2 |
| C、i>20°n=n+2 |
| D、i>20°n=n+1 |
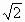 BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.