题目内容
(2005
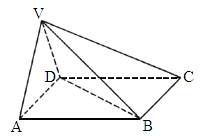
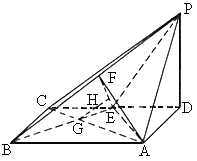
全国Ⅱ,20)如下图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点.(1)
求证:EF⊥平面PAB;(2)
设AB=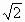 BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.
答案:略
解析:
提示:
解析:
|
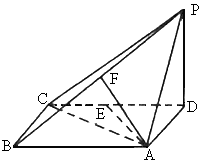
解析: (1)证明:如下图,连结EP,∵PD⊥底面ABCD,DE在平面ABCD内.∴PD⊥DE.又CE=ED,PD=AD=BC.∴Rt△BCE≌Rt△PDE.∴PE=BE.
∵ F为PB中点.∴ EF⊥PB.由垂线定理得 PA⊥AB.∴在 Rt△PAB中PF=AF,又 PE=BE=EA.∴△ EFP≌△EFA.∴ EF⊥FA.∵ PB、FA为平面PAB内的相交直线,∴EF⊥平面PAB.(2) 不妨设BC=1,则AD=PD=1,AB=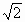 ,PA= ,PA=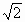 ,AC= ,AC=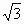 . .
∴△ PAB为等腰直角三角形,且PB=2,F为其斜边中点,BF=1.且AF⊥PB.∵ PB与平面AEF内两条相交直线EF、AF都垂直,∴ PB⊥平面AEF.连结 BE交AC于G,作GH∥BP交EF于H,则GH⊥平面AEF.∠GAH为AC与平面AEF所成的角.由△ EGC∽△BGA可知
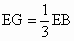 , ,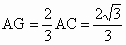 . .
由△ EGH∽△EBF可知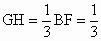 . .
∴ 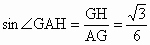 . .
∴ AC与面AEF所成的角为arcsin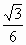 . . |
提示:
|
剖析:本题主要考查直线与平面垂直、直线与平面所成角的有关知识、及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力. |

练习册系列答案
相关题目
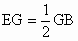
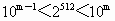 ,则m=_______(lg 2≈0.3010).
,则m=_______(lg 2≈0.3010).