题目内容
2.在△ABC中,设a=($\sqrt{3}$-1)c,$\frac{sinBcosC}{cosBsinC}$=$\frac{2a-c}{c}$,求三角形的三内角.分析 利用正弦定理,结合正弦的和角公式,求出B.利用a=($\sqrt{3}$-1)c,求出A,C.
解答 解:∵$\frac{sinBcosC}{cosBsinC}$=$\frac{2a-c}{c}$,
∴$\frac{sinBcosC}{cosBsinC}$=$\frac{2sinA-sinC}{sinC}$,
∴sinBcosC=2sinAcosB-sinCcosB,
移项利用正弦的和角公式得sin(B+C)=2sinAcosB=sinA,
∴cosB=$\frac{1}{2}$,
∴B=60°,
而a=($\sqrt{3}$-1)c,
∴sin(120°-C)=($\sqrt{3}$-1)sinC
∴tanC=2+$\sqrt{3}$.
∴C=75°,A=45°
点评 本题考查正弦定理,正弦的和角公式,考查学生的计算能力,正确运用公式是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
12.有一种细菌和一种病毒,每个细菌在每秒钟杀死一个病毒的同时自身分裂为2个,现有一个这样的细菌和500个病毒,则细菌将病毒全部杀死至少需要( )
| A. | 7秒钟 | B. | 8秒钟 | C. | 9秒钟 | D. | 10秒钟 |
14.实数a、b满足①2b≥a2-4a;②b≤$\sqrt{4a-{a}^{2}}$;③(|a-2|+|b|-2)(|a-2|+|b|-3)≤0这三个条件,则|a-b-6|的范围是( )
| A. | [2,4+2$\sqrt{2}$] | B. | [$\frac{3}{2}$,7] | C. | [$\frac{3}{2}$,4+2$\sqrt{2}$] | D. | [4-2$\sqrt{2}$,7] |
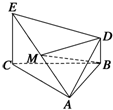 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,EC=CA=2BD,M是EA的中点.求证:
如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,EC=CA=2BD,M是EA的中点.求证: