题目内容
点(2,1)与(1,2)在函数f(x)=2ax+b的图象上,求f(x)的解析式.
解:∵(2,1)在函数f(x)=2ax+b的图象上,∴1=22a+b ,
又∵(1,2)在f(x)=2ax+b的图象上,∴2=2a+b ,
可得a=-1,b=2,∴f(x)=2-x+2.
f(x)的解析式:f(x)=2-x+2.
分析:把题中所给的2个点的坐标分别代入函数解析式,解方程组求出待定系数,从而得到函数解析式.
点评:本题考查用待定系数法求函数解析式,体现了代入得思想.
又∵(1,2)在f(x)=2ax+b的图象上,∴2=2a+b ,
可得a=-1,b=2,∴f(x)=2-x+2.
f(x)的解析式:f(x)=2-x+2.
分析:把题中所给的2个点的坐标分别代入函数解析式,解方程组求出待定系数,从而得到函数解析式.
点评:本题考查用待定系数法求函数解析式,体现了代入得思想.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
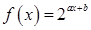 的图象上,则
的图象上,则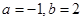 B.
B.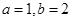
 D.
D.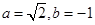
 的图象上,则
的图象上,则 B.
B.
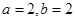 D.
D.