题目内容
6.已知函数f(x)是定义在区间[-a,a]上的奇函数,若g(x)=f(x)+2,则g(x)的最大值与最小值之和为( )| A. | 0 | B. | 2 | C. | 4 | D. | 不能确定 |
分析 运用奇函数的性质:函数的最值互为相反数,可设f(x)的最小值为m,则最大值为-m,代入g(x),计算即可得到所求和.
解答 解:由函数f(x)是定义在区间[-a,a]上的奇函数,
可设f(x)的最小值为m,则最大值为-m,
由g(x)=f(x)+2,可得g(x)的最小值为m+2,最大值为2-m,
则g(x)的最大值与最小值之和为m+2+2-m=4.
故选C.
点评 本题考查函数的奇偶性的运用,考查函数的最值的求法,注意运用奇函数的性质:函数的最值互为相反数,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
16.已知函数y=x2-6x+8在[1,a]为减函数,则a的取值范围是( )
| A. | a≤3 | B. | 1<a≤3 | C. | a≥3 | D. | 0≤a≤3 |
17.下列函数中,是奇函数且在区间(0,1)内单调递减的函数是( )
| A. | y=log${\;}_{\frac{1}{2}}$x | B. | $y=\frac{-1}{x}$ | C. | y=-x3 | D. | y=tanx |
16.如图所示,是某小朋友在用火柴拼图时呈现的图形,其中第1个图形用了3根火柴,第2个图形用了9根火柴,第3个图形用了18个火柴,…,第2014个图形用的火柴根数为( )


| A. | 2012×2015 | B. | 2013×2014 | C. | 2013×2015 | D. | 3021×2015 |
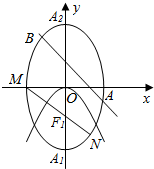 如图,M为椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点,F1是它的下焦点,F1也是抛物线x2=-4y的焦点,直线MF1与椭圆C的另一个交点为N,满足$\overrightarrow{M{F}_{1}}$=$\frac{5}{3}$$\overrightarrow{{F}_{1}N}$
如图,M为椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点,F1是它的下焦点,F1也是抛物线x2=-4y的焦点,直线MF1与椭圆C的另一个交点为N,满足$\overrightarrow{M{F}_{1}}$=$\frac{5}{3}$$\overrightarrow{{F}_{1}N}$