题目内容
解关于x的不等式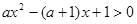
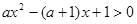
解：就a的范围进行讨论：
1)当a=0时，原不等式可化为：-x+1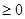
得不等式的解集
{
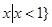
2)当a>0时，原不等式可化为：(x-1)(x-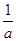
)<0
当a>1时，不等式的解集为：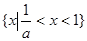
当0<a<1时，不等式的解集为：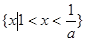
当a=1时，不等式的解集为: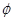
3),当a<0时，原不等式可化为：(x-1)(x-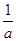)>0
解之得：
1)当a=0时，原不等式可化为：-x+1
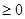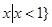
得不等式的解集{2)当a>0时，原不等式可化为：(x-1)(x-
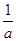)<0当a>1时，不等式的解集为：
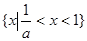
当0<a<1时，不等式的解集为：
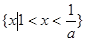
当a=1时，不等式的解集为:
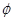
3),当a<0时，原不等式可化为：(x-1)(x-
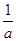)>0解之得：
本试题主要是考查了一元二次不等式的求解的问题，对于开口方向的讨论，以及根的大小的 讨论时解决本试题的关键所在，因此体现了数学中分类讨论思想的重要运用
练习册系列答案
相关题目
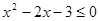的解集是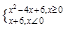 
则不等式f(x)>f(1)的解集是( )
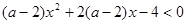对一切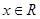
恒成立，则实数
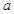的取值范围是（ ）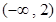
.
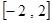
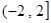
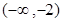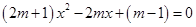有一正根和一负根，则实数
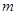的取值范围（ ）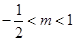
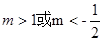
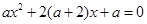有实数解，那么实数a的取值范围是____________．
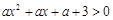对一切实数x恒成立，则实数a的取值范围是_______________．
的解集为
，则
值是（ ）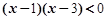
的解集为 _____ _____.