题目内容
(本小题满分12分)
如图,在四棱锥S—ABCD中,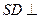 底面ABCD,底面ABCD是平行四边形,
底面ABCD,底面ABCD是平行四边形,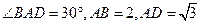 ,E是SC的中点。
,E是SC的中点。
(I)求证:SA//平面BDE;
(II)求证: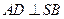 ;
;
(III)若SD=2,求二面角E—BD—C的余弦值。
解:
(Ⅰ)连结AC交BD于F,连结EF,
由ABCD是平行四边形 ,知F为AC的中点,
,知F为AC的中点,
又E为SC的中点,所以SA∥EF,
∵SAË平面BDE,EFÌ平面BDE,
∴SA∥平面BDE.…………………………………………………………………4分
(Ⅱ)由AB=2,AD=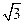 ,∠BAD=30°,及余弦定理得
,∠BAD=30°,及余弦定理得
取BD2=AB2+AD2-2AB·ADcos∠BAD=1,
∵AD2+BD2=AB2,∴AD⊥BD.
∵SD⊥平面ABCD,ADÌ平面ABCD,
∴AD⊥SD,
∴AD⊥平面SBD,又SBÌ平面SBD,
∴AD⊥SB.…………………………………………………………………………8分
(Ⅲ)取CD的中点G,连结EG,则EG⊥面BCD,且EG=1.
设三棱锥C—BDE的高为h,
在△BDE中,BD=1,DE=BE=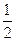 SC=
SC=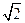 ,EF=
,EF=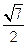 .
.
在Rt△BCD中,BD=1,BC=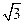 ,∠CBD=90°.
,∠CBD=90°.
∵VC—BDE=EE—BCD,
∴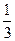 ·
·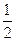 ·BD·EF·h=
·BD·EF·h=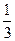 ·
·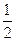 ·BD·BC·EG,
·BD·BC·EG,
∴h=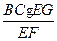 =
=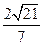 .…………………………………………………………12分
.…………………………………………………………12分
解析

练习册系列答案
相关题目