题目内容
已知空间四边形ABCD中,AB=CD=3,E、F分别是BC、AD上的点,并且BE∶EC=AF∶FD=1∶2,EF= ,求AB和CD所成角的余弦值.
,求AB和CD所成角的余弦值.
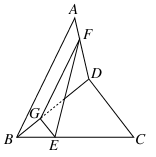
 ,求AB和CD所成角的余弦值.
,求AB和CD所成角的余弦值.
解:如图所示,在BD上取点G,
使BG∶GD=1∶2,
连接EG、FG.
在△BCD中,∵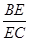 =
=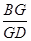 =
=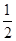 ,∴EG∥CD,
,∴EG∥CD,
且GE∶CD=1∶3,则EG=1,
同理FG∥AB,且FG∶AB=2∶3,则FG=2.
∴EG与FG所成的角即为AB与CD所成的角.
在△EFG中,EG=1,FG=2,EF= ,
,
由余弦定理得
cos∠EGF=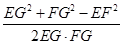 =-
=-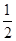 ,
,
∵异面直线所成角θ的范围是0°<θ≤90°,
∴cosθ≥0.
∴AB与CD所成角的余弦值为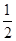 .
.
使BG∶GD=1∶2,
连接EG、FG.
在△BCD中,∵
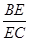 =
=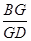 =
=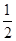 ,∴EG∥CD,
,∴EG∥CD,且GE∶CD=1∶3,则EG=1,
同理FG∥AB,且FG∶AB=2∶3,则FG=2.
∴EG与FG所成的角即为AB与CD所成的角.
在△EFG中,EG=1,FG=2,EF=
 ,
,由余弦定理得
cos∠EGF=
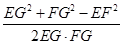 =-
=-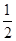 ,
,∵异面直线所成角θ的范围是0°<θ≤90°,
∴cosθ≥0.
∴AB与CD所成角的余弦值为
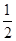 .
.
练习册系列答案
相关题目
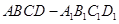 中,
中, 是
是 的中点.
的中点.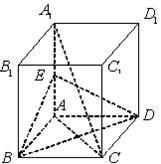
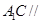 平面
平面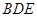 ;
;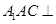 平面
平面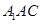 所成角的正弦值.
所成角的正弦值.
 、
、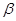 和直线
和直线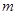 ,给出条件:①
,给出条件:①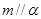 ;②
;②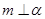 ;③
;③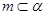 ;④
;④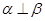 ;⑤
;⑤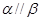 .
.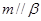 的是( )
的是( ) a⊥b
a⊥b