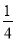题目内容
已知函数f(x)＝2sin ωx－4sin 2
＋2＋a(ω>0，a∈R)，且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
(1)求函数f(x)的最小正周期；
(2)若f(x)在区间[6,16]上的最大值为4，求a的值．
(1) 16 (2) a＝2.
【解析】(1)f(x)＝2sin ωx－4sin2
＋2＋a＝2sin ωx－2(1－cos ωx)＋2＋a＝2
sin 
＋a，∴2ω＋
＝
，得ω＝
，∴f(x)的最小正周期T＝
＝16.
(2)由(1)可得f(x)＝2
sin 
＋a，∵x∈[6,16]，∴
x＋
∈
，∴当
x＋
＝
，即x＝16时，f(x)最大，由2
sin 
＋a＝4，得a＝2.
练习册系列答案
相关题目
