题目内容
已知F、E分别是抛物线Y2=4x的焦点及准线与x轴的交点,M是曲线C上的任意一点,且满足|| ME |
| MF |
(I)求点M的轨迹C的方程;
(II)过点(
| 3 |
| 2 |
| OP |
| OA |
| OB |
分析:(I)由题意知,点E,F的坐标分别是(-1,0),(1,0),且|EF|=2,又|
|+|
| =4>2,轨迹C是以E、F为焦点的椭圆,且2a=4,2c=2,由此能求出轨迹C的方程.
(II)假设存在这样的直线l,使得四边形OAPB是矩形,则OA⊥OB,直线l过点(
,0),当直线l⊥x轴时,其方程为x=
,此时l与椭圆的两个交点为A(
,
) ,B(
,-
),由
•
≠0,OA与OB不垂直,故不存在这样的直线L.
| ME |
| MF |
(II)假设存在这样的直线l,使得四边形OAPB是矩形,则OA⊥OB,直线l过点(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 4 |
| 3 |
| 2 |
| ||
| 4 |
| OA |
| OB |
解答:解:(I)由题意知,点E,F的坐标分别是(-1,0),(1,0),且|EF|=2,
又|
|+|
| =4>2,
∴轨迹C是以E、F为焦点的椭圆,且2a=4,2c=2,
∴a=2,c=1,b2=3,
∴轨迹C的方程为
+
=1.
(II)假设存在这样的直线l,使得四边形OAPB是矩形,则OA⊥OB,
∵直线l过点(
,0),当直线l⊥x轴时,其方程为x=
,
此时l与椭圆的两个交点为A(
,
) ,B(
,-
),∴
•
≠0,
∴OA与OB不垂直,∴x=
不合题意.
当直线l不垂直于x轴时,设AB的方程为y=k(x-
),A(x1,y1),B坐标为(x2,y2);
联立y=k(x-
)与
+
=1可得,
+
=1,
若四边形OAPB是矩形,必有x1x2+y1y2=0,
易得不存在k的值满足,
故不存在这样的直线L.
又|
| ME |
| MF |
∴轨迹C是以E、F为焦点的椭圆,且2a=4,2c=2,
∴a=2,c=1,b2=3,
∴轨迹C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)假设存在这样的直线l,使得四边形OAPB是矩形,则OA⊥OB,
∵直线l过点(
| 3 |
| 2 |
| 3 |
| 2 |
此时l与椭圆的两个交点为A(
| 3 |
| 2 |
| ||
| 4 |
| 3 |
| 2 |
| ||
| 4 |
| OA |
| OB |
∴OA与OB不垂直,∴x=
| 3 |
| 2 |
当直线l不垂直于x轴时,设AB的方程为y=k(x-
| 3 |
| 2 |
联立y=k(x-
| 3 |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
k2(x-
| ||
| 3 |
若四边形OAPB是矩形,必有x1x2+y1y2=0,
易得不存在k的值满足,
故不存在这样的直线L.
点评:本题考查直线 和圆锥曲线的位置关系的综合运用,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目
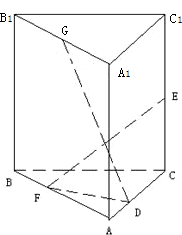 如图,在直三棱柱A1B1C1-ABC中,∠BAC=
如图,在直三棱柱A1B1C1-ABC中,∠BAC=| π |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[1,
| ||||||
D、[
|
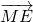 |+|
|+|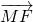 |=4.
|=4. ,0)作直线l与曲线C交于A、B两点.设
,0)作直线l与曲线C交于A、B两点.设 =
= +
+ ,是否存在这样的直线L,使得四边形OAPB是矩形?若存在,求出直线L的方程,若不存在,试说明理由.
,是否存在这样的直线L,使得四边形OAPB是矩形?若存在,求出直线L的方程,若不存在,试说明理由.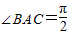 ,AB=AC=A1A=1,已知G与E分别是棱A1B1和CC1的中点,D与F分别是线段AC与AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围是( )
,AB=AC=A1A=1,已知G与E分别是棱A1B1和CC1的中点,D与F分别是线段AC与AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围是( )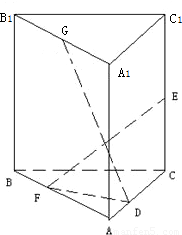
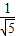 ,1)
,1) ,2)
,2)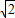 )
)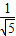 ,
,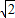 )
)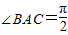 ,AB=AC=A1A=1,已知G与E分别是棱A1B1和CC1的中点,D与F分别是线段AC与AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围是( )
,AB=AC=A1A=1,已知G与E分别是棱A1B1和CC1的中点,D与F分别是线段AC与AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围是( )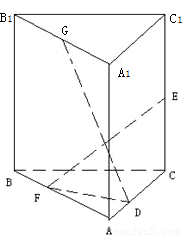
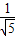 ,1)
,1) ,2)
,2)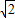 )
)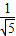 ,
,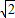 )
)