题目内容
如图,在直三棱柱A1B1C1-ABC中,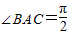 ,AB=AC=A1A=1,已知G与E分别是棱A1B1和CC1的中点,D与F分别是线段AC与AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围是( )
,AB=AC=A1A=1,已知G与E分别是棱A1B1和CC1的中点,D与F分别是线段AC与AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围是( )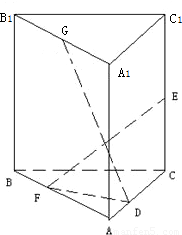
A.[
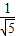 ,1)
,1)B.[
 ,2)
,2)C.[1,
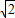 )
)D.[
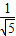 ,
,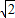 )
)
【答案】分析:建立空间直角坐标系,设出F、D的坐标,求出向量 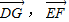 ,利用GD⊥EF求得关系式,写出DF的表达式,然后利用二次函数求最值即可.
,利用GD⊥EF求得关系式,写出DF的表达式,然后利用二次函数求最值即可.
解答: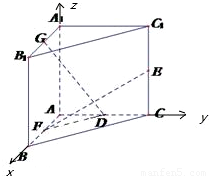 解:建立如图所示的空间直角坐标系,则A(0,0,0),E(0,1,
解:建立如图所示的空间直角坐标系,则A(0,0,0),E(0,1, ),
),
G( ,0,1),F(x,0,0),D(0,y,0)由于
,0,1),F(x,0,0),D(0,y,0)由于
GD⊥EF,所以 x+2y-1=0
DF=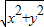 =
=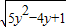 =
=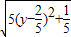
当y= 时,线段DF长度的最小值是
时,线段DF长度的最小值是 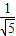
当y=1时,线段DF长度的最大值是2,
而不包括端点,故y=1不能取2;
故选B.
点评:本题考查棱柱的结构特征,考查空间想象能力,空间直角坐标系,数量积等知识,是中档题.
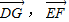 ,利用GD⊥EF求得关系式,写出DF的表达式,然后利用二次函数求最值即可.
,利用GD⊥EF求得关系式,写出DF的表达式,然后利用二次函数求最值即可.解答:
 解:建立如图所示的空间直角坐标系,则A(0,0,0),E(0,1,
解:建立如图所示的空间直角坐标系,则A(0,0,0),E(0,1, ),
),G(
 ,0,1),F(x,0,0),D(0,y,0)由于
,0,1),F(x,0,0),D(0,y,0)由于GD⊥EF,所以 x+2y-1=0
DF=
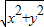 =
=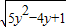 =
=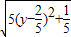
当y=
 时,线段DF长度的最小值是
时,线段DF长度的最小值是 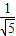
当y=1时,线段DF长度的最大值是2,
而不包括端点,故y=1不能取2;
故选B.
点评:本题考查棱柱的结构特征,考查空间想象能力,空间直角坐标系,数量积等知识,是中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,BC=CC1=AC=a
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,BC=CC1=AC=a 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2 (2012•重庆)如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
(2012•重庆)如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点. (2010•唐山二模)如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=2,AA1=4,M、N分别为CC1、A1C2的中点.
(2010•唐山二模)如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=2,AA1=4,M、N分别为CC1、A1C2的中点.