题目内容

2．已知log23=a，log35=b，试用a、b表示log1520．

分析 利用换底公式，可得log23=$\frac{lg3}{lg2}$=a，log35=$\frac{lg5}{lg3}$=$\frac{1-lg2}{lg3}$=b，进而lg2=$\frac{1}{ab+1}$，lg3=$\frac{a}{ab+1}$，再结合换底公式，可用a、b表示log1520．

解答 解：∵log23=$\frac{lg3}{lg2}$=a，log35=$\frac{lg5}{lg3}$=$\frac{1-lg2}{lg3}$=b，
∴lg2=$\frac{1}{ab+1}$，lg3=$\frac{a}{ab+1}$
∴log1520=$\frac{lg20}{lg15}$=$\frac{1+lg2}{lg3+lg5}$=$\frac{1+lg2}{lg3+（1-lg2）}$=$\frac{1+\frac{1}{ab+1}}{\frac{a}{ab+1}+（1-\frac{1}{ab+1}）}$=$\frac{ab+2}{a+ab}$

点评 本题考查的知识是对数的运算性质，换底公式，方程思想，难度中档．

练习册系列答案
相关题目
12．已知$\overrightarrow{a}$=（-1，3），$\overrightarrow{b}$=（1，y）．若$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°，则y=2或-$\frac{1}{2}$．
13．求与直线5x-3y+3=0平行，且与直线5x-3y+3=0的距离为$\sqrt{17}$的直线方程．
10．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$中，|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=4，|$\overrightarrow{a}$+$\overrightarrow{b}$|=6，则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{30}$．
17．设一直线上三点A，B，P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$（λ≠-1），O是平面内任意一点，则用$\overrightarrow{OA}$，$\overrightarrow{OB}$表示$\overrightarrow{OP}$式子为（　　）
A．$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ$\overrightarrow{OB}$B．$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+（1-λ）$\overrightarrow{OB}$
C．$\overrightarrow{OP}$=$\frac{1}{λ}$$\overrightarrow{OA}$+$\frac{1}{1+λ}$$\overrightarrow{OB}$D．$\overrightarrow{OP}$=$\frac{1}{1+λ}$$\overrightarrow{OA}$+$\frac{λ}{1+λ}$$\overrightarrow{OB}$
1．在四棱锥S-ABCD中，为了推出AB⊥BC，需从下列条件：
①SB⊥面ABCD；②SC⊥CD；③CD∥面SAB；④BC⊥CD中选出部分条件，这些条件可能是（　　）
A．②③B．①④C．②④D．③④
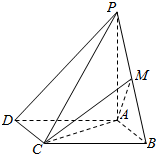8．如图：在四棱锥P-ABCD中，底面ABCD是平行四边形，BC⊥平面PAB，PA⊥AB，M为PB中点，PA=AD=2，AB=1．
（1）求证：PD∥面ACM；
（2）求VD-PMC．
5．已知函数f（x）=（sinωx+cosωx）2+$\sqrt{3}$（sin2ωx-cos2ωx），（ω＞0）的最小正周期为π．
（1）求ω的值及f（x）的单调递增区间；
（2）在锐角△ABC中，角ABC所对的边分别为abc，f （A）=$\sqrt{3}$+1，a=2，且b+c=4，求△ABC的面积．
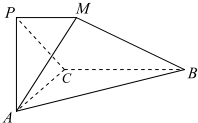6．在如图所示的多面体PMBCA中，平面PAC⊥平面ABC，△PAC是边长为2的正三角形，PM∥BC，且BC=4，$AB=2\sqrt{5}$．
（1）求证：PA⊥BC；
（2）若多面体PMBCA的体积为$2\sqrt{3}$，求PM的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网