题目内容
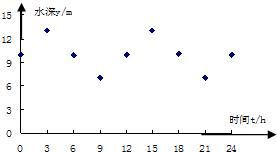 某港口的水深y(m)是时间t (0≤t≤24,单位:h)的函数,下表是该港口某一天从0:00时至24:00时记录的时间t与水深y的关系:
某港口的水深y(m)是时间t (0≤t≤24,单位:h)的函数,下表是该港口某一天从0:00时至24:00时记录的时间t与水深y的关系:
| t(h) | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| y(m) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)求出当天的拟合函数y=Asin(ωx+?)+h的表达式;
(2)如果某船的吃水深度(船底与水面的距离)为7m,船舶安全航行时船底与海底的距离不少于4.5m.那么该船在什么时间段能够进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间.(忽略离港所需时间)
(3)若某船吃水深度为8m,安全间隙(船底与海底的距离)为2.5.该船在3:00开始卸货,吃水深度以每小时0.5m的速度减少,那么该船在什么时间必须停止卸货,驶向较安全的水域?
解:(1)根据数据,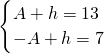 ,
,
∴A=3,h=10,
T=15-3=12,
∴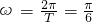 ,
,
∴y=3sin( x+?)+10
x+?)+10
将点(3,13)代入可得?=0
∴函数的表达式为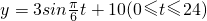
(2)由题意,水深y≥4.5+7,
即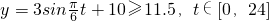 ,
,
∴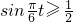 ,
,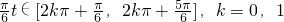 ,
,
∴t∈[1,5]或t∈[13,17];
所以,该船在1:00至5:00或13:00至17:00能安全进港.
若欲于当天安全离港,它在港内停留的时间最多不能超过16小时.
(3)设在时刻x船舶安全水深为y,则y=10.5-0.5(x-3)(x≥3),
这时水深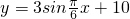 ,
,
若使船舶安全,则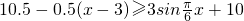 ,
,
即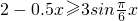 ,
,
∴3≤x≤7,
即该船在7:00必须停止卸货,驶向较安全的水域.
分析:(1)根据数据,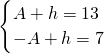 ,可得A=3,h=10,由T=15-3=12,可求ω=
,可得A=3,h=10,由T=15-3=12,可求ω= 将点(3,13)代入可得?=0,从而可求函数的表达式;
将点(3,13)代入可得?=0,从而可求函数的表达式;
(2)由题意,水深y≥4.5+7,即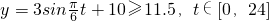 ,从而可求t∈[1,5]或t∈[13,17];
,从而可求t∈[1,5]或t∈[13,17];
(3)设在时刻x船舶安全水深为y,则y=10.5-0.5(x-3)(x≥3),若使船舶安全,则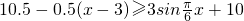 ,从而可得3≤x≤7,即该船在7:00必须停止卸货,驶向较安全的水域.
,从而可得3≤x≤7,即该船在7:00必须停止卸货,驶向较安全的水域.
点评:本题以表格数据为载体,考查三角函数模型的构建,考查解三角不等式,同时考查学生分析解决问题的能力.
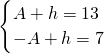 ,
,∴A=3,h=10,
T=15-3=12,
∴
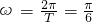 ,
,∴y=3sin(
 x+?)+10
x+?)+10将点(3,13)代入可得?=0
∴函数的表达式为
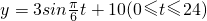
(2)由题意,水深y≥4.5+7,
即
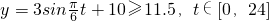 ,
,∴
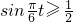 ,
,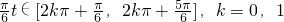 ,
,∴t∈[1,5]或t∈[13,17];
所以,该船在1:00至5:00或13:00至17:00能安全进港.
若欲于当天安全离港,它在港内停留的时间最多不能超过16小时.
(3)设在时刻x船舶安全水深为y,则y=10.5-0.5(x-3)(x≥3),
这时水深
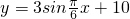 ,
,若使船舶安全,则
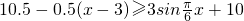 ,
,即
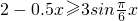 ,
,∴3≤x≤7,
即该船在7:00必须停止卸货,驶向较安全的水域.
分析:(1)根据数据,
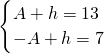 ,可得A=3,h=10,由T=15-3=12,可求ω=
,可得A=3,h=10,由T=15-3=12,可求ω= 将点(3,13)代入可得?=0,从而可求函数的表达式;
将点(3,13)代入可得?=0,从而可求函数的表达式;(2)由题意,水深y≥4.5+7,即
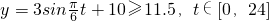 ,从而可求t∈[1,5]或t∈[13,17];
,从而可求t∈[1,5]或t∈[13,17];(3)设在时刻x船舶安全水深为y,则y=10.5-0.5(x-3)(x≥3),若使船舶安全,则
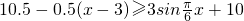 ,从而可得3≤x≤7,即该船在7:00必须停止卸货,驶向较安全的水域.
,从而可得3≤x≤7,即该船在7:00必须停止卸货,驶向较安全的水域.点评:本题以表格数据为载体,考查三角函数模型的构建,考查解三角不等式,同时考查学生分析解决问题的能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
下表给出的是某港口在某季节每天几个时刻的水深.
| 时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| 水深/m | 5.0 | 8.0 | 5.0 | 2.0 | 5.0 | 8.0 | 5.0 | 2.0 | 5.0 |
(2)若一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有2.5m的安全间隙(船底与海底的距离),试用(1)中的函数关系判断该船何时能进入港口?
某港口的水深y(m)是时间t (0≤t≤24,单位:h)的函数,下表是该港口某一天从0:00时至24:00时记录的时间t与水深y的关系:
经长时间的观察,水深y与t的关系可以用y=Asin(ωx+ϕ)+h拟合.根据当天的数据,完成下面的问题:
(1)求出当天的拟合函数y=Asin(ωx+ϕ)+h的表达式;
(2)如果某船的吃水深度(船底与水面的距离)为7m,船舶安全航行时船底与海底的距离不少于4.5m.那么该船在什么时间段能够进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间.(忽略离港所需时间)
(3)若某船吃水深度为8m,安全间隙(船底与海底的距离)为2.5.该船在3:00开始卸货,吃水深度以每小时0.5m的速度减少,那么该船在什么时间必须停止卸货,驶向较安全的水域?

| t(h) | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| y(m) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)求出当天的拟合函数y=Asin(ωx+ϕ)+h的表达式;
(2)如果某船的吃水深度(船底与水面的距离)为7m,船舶安全航行时船底与海底的距离不少于4.5m.那么该船在什么时间段能够进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间.(忽略离港所需时间)
(3)若某船吃水深度为8m,安全间隙(船底与海底的距离)为2.5.该船在3:00开始卸货,吃水深度以每小时0.5m的速度减少,那么该船在什么时间必须停止卸货,驶向较安全的水域?

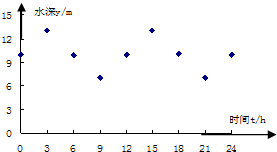 某港口的水深y(m)是时间t (0≤t≤24,单位:h)的函数,下表是该港口某一天从0:00时至24:00时记录的时间t与水深y的关系:
某港口的水深y(m)是时间t (0≤t≤24,单位:h)的函数,下表是该港口某一天从0:00时至24:00时记录的时间t与水深y的关系: