题目内容
1.△ABC所在平面上一点P满足$\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{AB}$,若△ABP的面积为6,则△ABC的面积为12.分析 由已知中P是△ABC所在平面内一点,且满足$\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{AB}$,我们根据向量加法的三角形法则可得$\overrightarrow{AB}$=2$\overrightarrow{PO}$,C到直线AB的距离等于P到直线AB的距离的2倍,故S△ABC=2S△ABP,结合已知中△ABP的面积为6,即可得到答案.
解答  解:取AC的中点O,则
解:取AC的中点O,则
∵$\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{AB}$,
∴$\overrightarrow{AB}$=2$\overrightarrow{PO}$,
∴C到直线AB的距离等于P到直线AB的距离的2倍
故S△ABC=2S△ABP=12
故答案为:12
点评 本题考查的知识点是向量的加减法及其几何意义,其中根据$\overrightarrow{AB}$=2$\overrightarrow{PO}$,得到S△ABC=2S△ABP,是解答本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
12.为了计算1×3×5×7×…×21的结果,设计如图所示的程序框图,则判断框内可填入的条件是( )

| A. | n≤9 | B. | n≤10 | C. | n≤11 | D. | n≤12 |
6.如图所示,在复平面内,点A对应的复数为z,则复数z2等于( )


| A. | 3-4i | B. | 3+4i | C. | -3+4i | D. | -3-4i |
13. 如图所示,在复平面内,点A对应的复数为z,则复数z2等于( )
如图所示,在复平面内,点A对应的复数为z,则复数z2等于( )
 如图所示,在复平面内,点A对应的复数为z,则复数z2等于( )
如图所示,在复平面内,点A对应的复数为z,则复数z2等于( )| A. | 3-4i | B. | -3-4i | C. | -3+4i | D. | 3+4i |
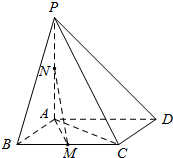 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.