题目内容
(本题12分)已知A、B、C是三角形ABC的三内角,且 ,
, ,并且
,并且
(Ⅰ)求角A的大小。
(Ⅱ) ,求
,求 的递增区间。
的递增区间。
【答案】
(1) 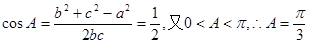
(2) 
【解析】解:(Ⅰ)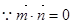
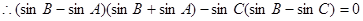
即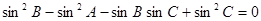 …………2分
…………2分
由正弦定理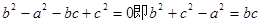 …………4分
…………4分
由余弦定理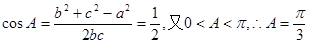 …………6分
…………6分
(Ⅱ)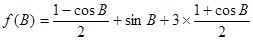
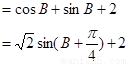 …………8分
…………8分
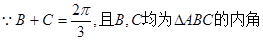
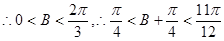
又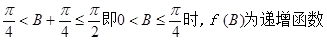
即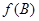 的递增区间为
的递增区间为 …………12分
…………12分

练习册系列答案
相关题目
 ,圆C与椭圆E:
,圆C与椭圆E:  有一个公共点A(3,1),
有一个公共点A(3,1), 分别是椭圆的左、右焦点;
分别是椭圆的左、右焦点; 与圆C能否相切,若能,求出椭
与圆C能否相切,若能,求出椭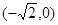 ,B
,B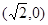 连线的斜率的积为定值
连线的斜率的积为定值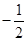 ,
,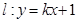 与曲线C交于M、N两点,当|MN|=
与曲线C交于M、N两点,当|MN|=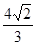 时,求直线
时,求直线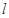 的方程。
的方程。 ,集合A
,集合A R
R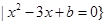 ,
,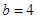 时,存在集合M使得A
时,存在集合M使得A M
M A=
A=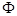 ?若能,求实数
?若能,求实数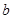 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.