题目内容
已知数列 中,
中, 是
是 的前
的前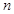 项和,且
项和,且 是
是 与
与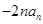 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数.
(1)求 ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.
 中,
中, 是
是 的前
的前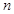 项和,且
项和,且 是
是 与
与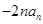 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数.(1)求
 ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.(1)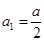 ,
,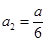 ,
,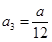 ;(2)见解析.
;(2)见解析.
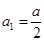 ,
,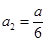 ,
,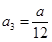 ;(2)见解析.
;(2)见解析.(1)先确定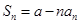 ,然后要以先求出a1,进而可以求出a2,a3;
,然后要以先求出a1,进而可以求出a2,a3;
(2)根据第(1)求出的结果进行猜想.然后再利用数学归纳法证明时两个步骤缺一不可.
解: (1)由题意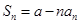 ,
,
当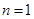 时,
时,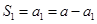 , ∴
, ∴ 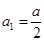 ;
;
当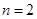 时,
时,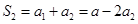 , ∴
, ∴ 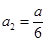 ;
;
当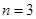 时,
时,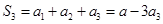 , ∴
, ∴ 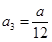 ;
;
(2)猜想: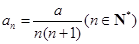 .
.
证明:①当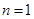 时,由(1)可知等式成立;
时,由(1)可知等式成立;
②假设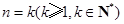 时等式成立,即:
时等式成立,即: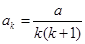 ,
,
则当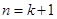 时,
时,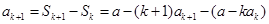 ,
,
∴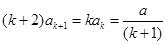 , ∴
, ∴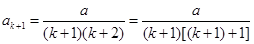 ,
,
即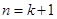 时等式也成立.
时等式也成立.
综合①②知: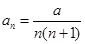 对任意
对任意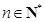 均成立.
均成立.
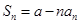 ,然后要以先求出a1,进而可以求出a2,a3;
,然后要以先求出a1,进而可以求出a2,a3;(2)根据第(1)求出的结果进行猜想.然后再利用数学归纳法证明时两个步骤缺一不可.
解: (1)由题意
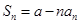 ,
, 当
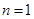 时,
时,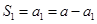 , ∴
, ∴ 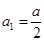 ;
; 当
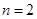 时,
时,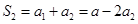 , ∴
, ∴ 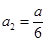 ;
; 当
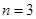 时,
时,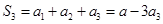 , ∴
, ∴ 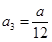 ;
; (2)猜想:
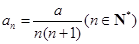 .
. 证明:①当
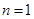 时,由(1)可知等式成立;
时,由(1)可知等式成立; ②假设
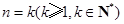 时等式成立,即:
时等式成立,即: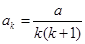 ,
, 则当
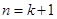 时,
时,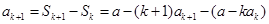 ,
,∴
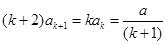 , ∴
, ∴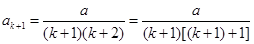 ,
, 即
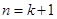 时等式也成立.
时等式也成立. 综合①②知:
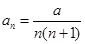 对任意
对任意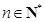 均成立.
均成立. 
练习册系列答案
相关题目
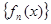 满足:
满足: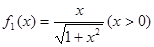 ,
,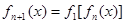
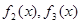 ;
;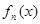 的表达式,并证明你的结论.
的表达式,并证明你的结论.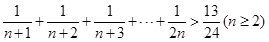 的过程中,由
的过程中,由 递推到
递推到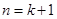 时的不等式左边.
时的不等式左边.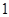 项
项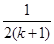
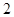 项
项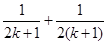
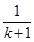 ”
”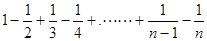 (n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.
(n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.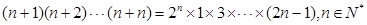 ”时,从假设
”时,从假设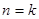 推证
推证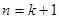 成立时,可以在
成立时,可以在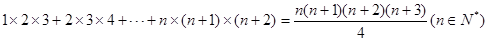 .
.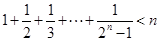 (
(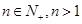 )时,第一步应验证不等式( )
)时,第一步应验证不等式( )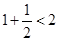
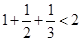
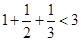

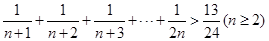 的过程中,
的过程中,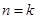 递推到
递推到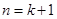 时的不等式左边( ).
时的不等式左边( ).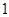 项
项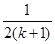
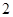 项
项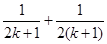
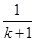 ”
”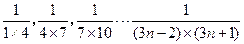 ,计算
,计算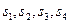 ,猜想
,猜想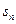 的表达式,并用数学归纳法证明猜想的正确性
的表达式,并用数学归纳法证明猜想的正确性