题目内容
(1)设0<x<1,求函数y=
的最大值
(2)已知x>0,y>0,x+y=1求
+
的最小值.
| x(1-x) |
(2)已知x>0,y>0,x+y=1求
| 1 |
| x |
| 1 |
| y |
(1)∵0<x<1,
函数y=
≤
=
当且仅当x=
时,ymax=
(2)∵x>0,y>0,x+y=1
则
+
=(
+
)(x+y)=2+
+
≥2+2
=4
当且仅当
=
即x=y=
时取等号
故
+
的最小值4
函数y=
| x(1-x) |
| x+1-x |
| 2 |
| 1 |
| 2 |
当且仅当x=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵x>0,y>0,x+y=1
则
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| y |
| x |
| x |
| y |
|
当且仅当
| y |
| x |
| x |
| y |
| 1 |
| 2 |
故
| 1 |
| x |
| 1 |
| y |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
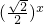 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是 ,1)
,1) -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)