题目内容
(1)设0<x<1,a>0且a≠1,比较|loga(1-x)|和|loga(1+x)|的大小;
(2)设a>0,x=
(a
-a-
),试求(x+
)n的值.
(2)设a>0,x=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1+x2 |
分析:(1)由于|loga(1-x)|和|loga(1+x)|都大于零,再由 0<x<1可得 log(1+x)(1-x)<0.化简
为log(1+x)
>1,从而得到|loga(1-x)|>|loga(1+x)|.
(2)根据 x=
(a
-a-
),化简 1+x2 为(a
+a-
)2,从而得
=
,代入要求的式子化简得到结果.
| |loga(1-x)| |
| |loga(1+x)| |
| 1+x |
| 1-x2 |
(2)根据 x=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1+x2 |
a
| ||||
| 2 |
解答:解:(1)由于|loga(1-x)|和|loga(1+x)|都大于零,再由 0<x<1可得0<1-x<1,1+x>1,故 log(1+x)(1-x)<0.
由于
=|log(1+x)(1-x)|=-log(1+x)(1-x)=log(1+x) (
)=log(1+x)
,再由上可得 0<1-x2<1,∴
>1+x,
∴log(1+x)
>log(1+x)(1+x)=1,∴|loga(1-x)|>|loga(1+x)|.
(2)∵x=
(a
-a-
),∴1+x2=1+
(a
-2 + a-
)=
(a
+2 + a-
)=
(a
+a-
)2,故
=
,
∴(x+
)n=[
(a
-a-
)+
(a
+a-
)]n=(a
)n=a.
由于
| |loga(1-x)| |
| |loga(1+x)| |
| 1 |
| 1-x |
| 1+x |
| 1-x2 |
| 1+x |
| 1-x2 |
∴log(1+x)
| 1+x |
| 1-x2 |
(2)∵x=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| 4 |
| 2 |
| n |
| 2 |
| n |
| 1 |
| 4 |
| 2 |
| n |
| 2 |
| n |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n |
| 1+x2 |
a
| ||||
| 2 |
∴(x+
| 1+x2 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
点评:本题主要考查对数函数的单调性和特殊点,用作商比较法比较两个正数的大小,分数指数幂的运算性质的应用,求得
=
,是解题的关键,属于中档题.
| 1+x2 |
a
| ||||
| 2 |

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
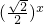 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是 ,1)
,1) -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)