题目内容
若函数f（x）=|x-2|+|x+2|的最小值为n，则（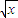
-
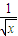）n的展开式中的常数项是（ ）A．第二项
B．第三项
C．第四项
D．第五项
【答案】分析：由绝对值的几何意义知函数f（x）=|x-2|+|x+2|的最小值为4，写出二项式的展开式的通项，看出当变量x的指数是0时，求出n的值，得到项数．
解答：解：由绝对值的几何意义知函数f（x）=|x-2|+|x+2|的最小值为4，
∴n=4，
∴（
-
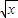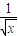）n=（
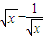）4
∴二项式的展开式是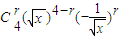
=
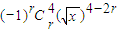
∴当4-2r=0时，r=2
展开式是一个常数项，
这是展开式的第三项，
故选B．
点评：本题考查二项式系数的性质及绝对值的几何意义，本题解题的关键是写出二项式的通项，所有的问题都可以在通项中解决．
解答：解：由绝对值的几何意义知函数f（x）=|x-2|+|x+2|的最小值为4，
∴n=4，
∴（
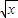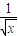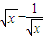-）n=（）4∴二项式的展开式是
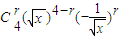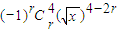
=∴当4-2r=0时，r=2
展开式是一个常数项，
这是展开式的第三项，
故选B．
点评：本题考查二项式系数的性质及绝对值的几何意义，本题解题的关键是写出二项式的通项，所有的问题都可以在通项中解决．
练习册系列答案
相关题目
若函数f（x）（x∈R）为奇函数，且存在反函数f-1（x）（与f（x）不同），F(x)=
，则下列关于函数F（x）的奇偶性的说法中正确的是（ ）
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F（x）是奇函数非偶函数 |
| B、F（x）是偶函数非奇函数 |
| C、F（x）既是奇函数又是偶函数 |
| D、F（x）既非奇函数又非偶函数 |