题目内容
9. 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.(Ⅰ)当∠PEC=75°时,求∠PDF的度数;
(Ⅱ)求PE•PF的值.
分析 (Ⅰ)连结BD,则∠BDA=90°,利用∠CDB=∠CAB,即可证明结论;
(Ⅱ)利用割线定理,即可求出PE•PF的值.
解答 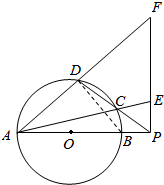 解:(Ⅰ)连结BD,则∠BDA=90°…(1分)
解:(Ⅰ)连结BD,则∠BDA=90°…(1分)
∵∠CDB=∠CAB…(2分)
∠PEC=90°-∠CAB,…(3分)
∠PDF=90°-∠CDB…(4分)
∴∠PEC=∠PDF=75°; (5分)
(Ⅱ)由(Ⅰ)得:∠PEC=∠PDF,
∴D,C,E,F四点共圆,…(7分)
∵AB=10,P是AB延长线上一点,BP=2,
∴PE•PF=PC•PD=PB•PA=2×12=24.(10分)
点评 本题考查四点共圆是证明,考查割线定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
9.函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x\\;x≥1}\\{{2}^{x}\\;x<1}\end{array}\right.$的值域为( )
| A. | (-∞,0] | B. | (-∞,2) | C. | [0,+∞) | D. | (2,+∞) |
18.已知球面上有A、B、C三点,BC=2$\sqrt{3}$,AB=AC=2,若球的表面积为20π,则球心到平面ABC的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
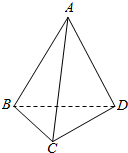 如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,
如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2, 如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.
如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C. 如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( )
如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( ) 如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.
如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.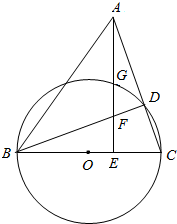 如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.
如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.