题目内容
(本小题满分12分)如图,在四棱锥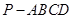 中,底面
中,底面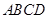 为菱形,
为菱形, ,
, 为
为 的中点。
的中点。
(1)若 ,求证:平面
,求证:平面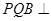 平面
平面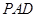 ;
;
(2)点 在线段
在线段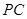 上,
上,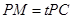 ,试确定
,试确定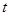 的值,使
的值,使 平面
平面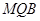 ;
;

【答案】
(1)见解析;(2)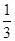 .
.
【解析】第一问中利用线面垂直的判定定理和面面垂直的判定定理得到证明,关键是证明AD⊥平面PQB, AD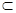 平面PAD
平面PAD
第二问中,先猜想t的值,然后加以证明。利用三角形相似得到相似比,然后可以分析证明。
解:(1)连BD,四边形ABCD菱形,
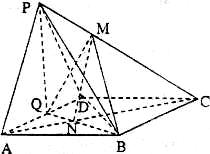
∵AD⊥AB, ∠BAD=60°
△ABD为正三角形, Q为AD中点, ∴AD⊥BQ
∵PA=PD,Q为AD的中点,AD⊥PQ
又BQ∩PQ=Q ∴AD⊥平面PQB, AD 平面PAD
平面PAD
∴平面PQB⊥平面PAD;……………………6分
(2)当t=1/3时,PA//平面MQB
下面证明,若PA//平面MQB,连AC交BQ于N
由AQ//BC可得,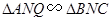 ,
,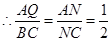
因为PA//平面MQB
, 平面PAC,平面
平面PAC,平面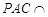 平面MQB=MN,所以PA//MN
平面MQB=MN,所以PA//MN
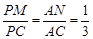 即:PM=1/3PC 故 t=1/3;……………………12分
即:PM=1/3PC 故 t=1/3;……………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目