题目内容
15.试推导焦点在y轴上的椭圆的标准方程:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1(a>b>0)$.分析 运用椭圆的定义:到两定点F1(0,-c),F2(0,c)(c>0)距离之和为定值2a(a>c)的点P的轨迹为椭圆.设P(x,y),由两点间的距离公式,运用移项和两边平方,化简整理,再令a2-c2=b2,即可得到所求椭圆方程.
解答 解:到两定点F1(0,-c),F2(0,c)(c>0)距离之和
为定值2a(a>c)的点P的轨迹为椭圆.
设P(x,y),则$|P{F_1}|+|P{F_2}|=2a=\sqrt{{x^2}+{{(y+c)}^2}}+\sqrt{{x^2}+{{(y-c)}^2}}$
∴$2a-\sqrt{{x^2}+{{(y+c)}^2}}=\sqrt{{x^2}+{{(y-c)}^2}}$,
∴${(2a-\sqrt{{x^2}+{{(y+c)}^2}})^2}={\sqrt{{x^2}+{{(y-c)}^2}}^2}$,
∴$4{a^2}+{x^2}+{(y+c)^2}-4a\sqrt{{x^2}+{{(y+c)}^2}}={x^2}+{(y-c)^2}$
∴$4{a^2}+{x^2}+{(y+c)^2}-4a\sqrt{{x^2}+{{(y+c)}^2}}={x^2}+{(y-c)^2}$,
∴$a+\frac{c}{a}y=\sqrt{{x^2}+{{(y+c)}^2}}$(由定义可得y∈[-a,a],所以$a+\frac{c}{a}y>0)$,
∴${a^2}+2cy+\frac{c^2}{a^2}{y^2}={x^2}+{(y+c)^2}$
∴${x^2}+\frac{{{a^2}-{c^2}}}{a^2}{y^2}={a^2}-{c^2}$,即$\frac{x^2}{{{a^2}-{c^2}}}+\frac{y^2}{a^2}=1$,
又a>c,不妨令a2-c2=b2,
∴焦点在y轴上的椭圆的标准方程:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(a>b>0)$.
点评 本题考查椭圆的方程的推导,注意运用定义法,考查化简整理的运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | {1} | B. | [0,1] | C. | (0,1] | D. | [0,1) |
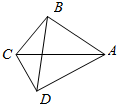 如图,在平面四边形ABCD中,若AB=2,CD=3,则$({\overrightarrow{AC}+\overrightarrow{DB}})•({\overrightarrow{AB}+\overrightarrow{CD}})$=( )
如图,在平面四边形ABCD中,若AB=2,CD=3,则$({\overrightarrow{AC}+\overrightarrow{DB}})•({\overrightarrow{AB}+\overrightarrow{CD}})$=( )