题目内容
椭圆C：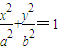
（a＞b＞0）的左、右焦点分别为F1（-1，0）、F2（1，0），O是坐标原点，C的右顶点和上顶点分别为A、B，且|AB|=3．（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线x=ky+1与C交于相异两点M、N，且
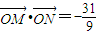，求k．
【答案】分析：（Ⅰ）利用椭圆的焦点坐标，及|AB|=3，建立方程组，即可求得椭圆C的方程；
（Ⅱ）直线x=ky+1代入椭圆方程，消去x可得一元二次方程，利用韦达定理及向量条件，即可求得结论．
解答：解：（Ⅰ）由题意，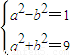
，∴a2=5，b2=4
∴椭圆C的方程为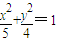
；
（Ⅱ）直线x=ky+1代入椭圆方程，消去x可得（5k2+4）y2+8ky-16=0
设M（x1，y1），N（x2，y2），则y1+y2=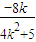
，y1y2=
∴
∵
∴
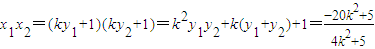
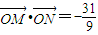
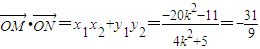
∴k2=1，从而k=±1
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查向量知识，考查韦达定理的运用，联立方程，正确运用韦达定理是关键．
（Ⅱ）直线x=ky+1代入椭圆方程，消去x可得一元二次方程，利用韦达定理及向量条件，即可求得结论．
解答：解：（Ⅰ）由题意，
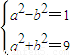，∴a2=5，b2=4∴椭圆C的方程为
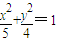；（Ⅱ）直线x=ky+1代入椭圆方程，消去x可得（5k2+4）y2+8ky-16=0
设M（x1，y1），N（x2，y2），则y1+y2=
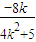，y1y2=∴
∵
∴
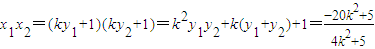
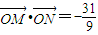
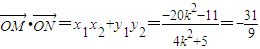
∴k2=1，从而k=±1
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查向量知识，考查韦达定理的运用，联立方程，正确运用韦达定理是关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
与椭圆C相交于两个不同点A、B，与直线2x+y-2=0交于点Q，若→AP=λ→PB，→AQ =μ→QB，求λ+μ的值
圆C: 
+
=1（a＞b＞0）的离心率e=
，且椭圆经过点N（2，-3）．
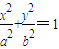（a＞b＞0）的长轴长是短轴长的两倍，焦距为
．
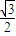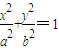（a＞b＞0）．
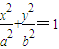（a＞b＞0）的短轴的一个端点，F为椭圆C的一个焦点，O为坐标原点，记∠BFO=θ．当椭圆C同时满足下列两个条件：①
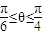；②a2+b2=2a2b2．求椭圆长轴的取值范围．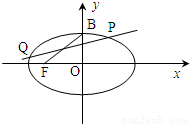
+
=1(a＞b＞0)，直线y=x+
与以原点为圆心，以椭圆C的短半轴长为半径的圆相切，F1，F2为其左、右焦点，P为椭圆C上任一点，△F1PF2的重心为G，内心为I，且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L：y=kx+m(k≠0)与椭圆C交于不同两点A，B且线段AB的垂直平分线过定点C(
，0)求实数k的取值范围。