题目内容
已知函数 .
.
(1)求函数 在
在 上的最大值和最小值;
上的最大值和最小值;
(2)求证:当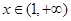 时,函数
时,函数 的图像在
的图像在 的下方.
的下方.
 .
.(1)求函数
 在
在 上的最大值和最小值;
上的最大值和最小值;(2)求证:当
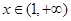 时,函数
时,函数 的图像在
的图像在 的下方.
的下方.(1) 的最小值是
的最小值是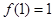 ,最大值是
,最大值是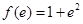 ;(2)证明详见解析.
;(2)证明详见解析.
 的最小值是
的最小值是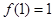 ,最大值是
,最大值是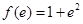 ;(2)证明详见解析.
;(2)证明详见解析.试题分析:(1)先求导函数,由导函数的符号确定
 在
在 上的单调性,进而确定函数的最值即可;(2)本题的实质是证明
上的单调性,进而确定函数的最值即可;(2)本题的实质是证明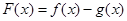 在区间
在区间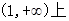 恒成立,然后利用导数研究其最大值即可.
恒成立,然后利用导数研究其最大值即可.试题解析:(1)∵
 ,∴
,∴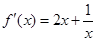
∵
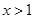 时,
时,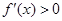 ,故
,故 在
在 上是增函数
上是增函数∴
 的最小值是
的最小值是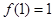 ,最大值是
,最大值是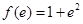
(2)证明:令
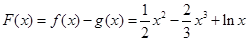
则
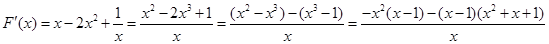
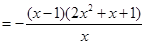
当
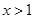 时,
时,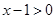 ,而
,而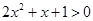
∴
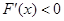
∴
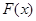 在
在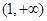 上是减函数
上是减函数∴
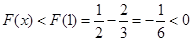 ,即
,即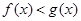
∴当
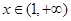 时,函数
时,函数 的图像总在
的图像总在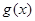 的图像的下方.
的图像的下方.
练习册系列答案
相关题目
 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和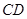 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当 ,高
,高 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大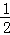 )
) 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 :②
:②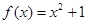 :③
:③ ;④
;④ ⑤
⑤ 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( ) (
( 为实常数).
为实常数). 在区间
在区间 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数 ,若不等式
,若不等式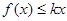 在
在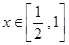 有解,求
有解,求 的取值范围.
的取值范围.
 满足:对定义域内的任意
满足:对定义域内的任意 ,都有
,都有 ,则函数
,则函数



 ,则
,则 在
在 上的零点个数( )
上的零点个数( )