题目内容
某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)。若安检不合格,则必须进行整改。若整改后经复查仍不合格,则强行关闭。设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率是0.8,计算(结果精确到0.01),
(Ⅰ)恰好有两家煤矿必须整改的概率;
(Ⅱ)平均有多少家煤矿必须整改;
(Ⅲ)至少关闭一家煤矿的概率。
(Ⅰ)恰好有两家煤矿必须整改的概率;
(Ⅱ)平均有多少家煤矿必须整改;
(Ⅲ)至少关闭一家煤矿的概率。
解:(Ⅰ)每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的,
所以恰好有两家煤矿必须整改的概率是 ;
;
(Ⅱ)由题设,必须整改的煤矿数ξ服从二项分布B(5,0.5),
从而ξ的数学期望是Eξ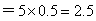 ,
,
即平均有2.50家煤矿必须整改;
(Ⅲ)某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,
所以该煤矿被关闭的概率是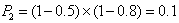 ,
,
从而该煤矿不被关闭的概率是0.9,
由题意,每家煤矿是否被关闭是相互独立的,
所以至少关闭一家煤矿的概率是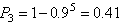 。
。
所以恰好有两家煤矿必须整改的概率是
 ;
;(Ⅱ)由题设,必须整改的煤矿数ξ服从二项分布B(5,0.5),
从而ξ的数学期望是Eξ
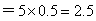 ,
,即平均有2.50家煤矿必须整改;
(Ⅲ)某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,
所以该煤矿被关闭的概率是
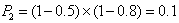 ,
,从而该煤矿不被关闭的概率是0.9,
由题意,每家煤矿是否被关闭是相互独立的,
所以至少关闭一家煤矿的概率是
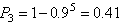 。
。 
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目