题目内容
已知直线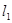 的方程为3x+4y-12=0,求满足下列条件的直线
的方程为3x+4y-12=0,求满足下列条件的直线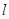 的方程.
的方程.
(1)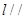
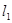 ,且直线
,且直线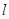 过点(-1,3);
过点(-1,3);
(2)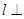
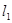 ,且
,且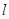 与两坐标轴围成的三角形面积为4.
与两坐标轴围成的三角形面积为4.
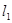 的方程为3x+4y-12=0,求满足下列条件的直线
的方程为3x+4y-12=0,求满足下列条件的直线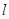 的方程.
的方程.(1)
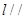
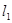 ,且直线
,且直线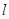 过点(-1,3);
过点(-1,3);(2)
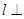
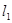 ,且
,且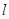 与两坐标轴围成的三角形面积为4.
与两坐标轴围成的三角形面积为4.(1)3x+4y-9=0(2)y=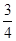 (x+
(x+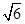 )或y=
)或y=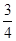 (x-
(x-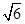 )
)
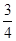 (x+
(x+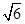 )或y=
)或y=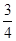 (x-
(x-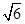 )
)试题分析:解:(1)直线
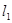 :3x+4y-12=0,
:3x+4y-12=0,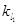 =-
=-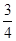 ,又∵
,又∵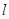 ∥
∥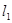 ,∴
,∴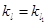 =-
=- 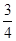 .
.∴直线
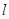 :y=-
:y=-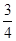 (x+1)+3,即3x+4y-9=0.
(x+1)+3,即3x+4y-9=0.(2)∵
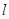 ⊥
⊥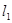 ,∴
,∴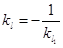 =
=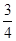 .设
.设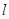 在x轴上截距为b,则
在x轴上截距为b,则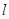 在y轴上截距为-
在y轴上截距为-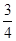 b,由题意可知,S=
b,由题意可知,S=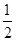 |b|·|-
|b|·|-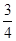 b|=4,∴b=±
b|=4,∴b=±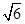 .∴直线
.∴直线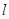 :y=
:y=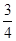 (x+
(x+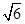 )或y=
)或y=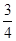 (x-
(x-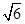 ).
).点评:主要是考查了直线方程的求解,以及三角形面积公式的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
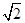
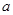 ,1+
,1+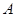 ,
,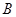 的坐标分别是
的坐标分别是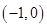 ,
,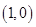 .直线
.直线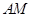 ,
,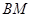 相交于点
相交于点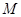 ,且它们的斜率之积为
,且它们的斜率之积为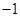 .
.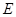 的方程;
的方程;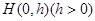 的两直线
的两直线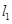 和
和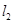 与轨迹
与轨迹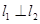 ,求
,求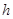 的值;
的值;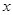 轴上是否存在两个定点
轴上是否存在两个定点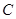 ,
,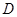 ,使得点
,使得点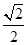 ,若存在,求出定点
,若存在,求出定点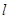 的参数方程为
的参数方程为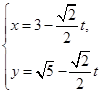 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 。
。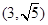 ,求|PA|+|PB|。
,求|PA|+|PB|。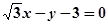 的倾斜角为_______________
的倾斜角为_______________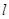 过点
过点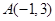 ,且与直线
,且与直线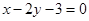 垂直,则直线
垂直,则直线