题目内容
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,若a=5![]() sin(B
sin(B![]() ),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
A.![]() 1B.
1B.![]() C.
C.![]() 1D.
1D.![]()
【答案】D
【解析】
首先根据条件解△ABC可得:C![]() 和△ABC外接圆的半径R
和△ABC外接圆的半径R![]() ,由此建立直角坐标系,可得:.A(
,由此建立直角坐标系,可得:.A(![]() ,0),B(
,0),B(![]() ,0),外心O为(0,
,0),外心O为(0,![]() ),重心G
),重心G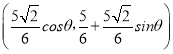 .从而求得|OG|2
.从而求得|OG|2![]() sinθ
sinθ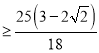 ,即可得解.
,即可得解.
A=5![]() sin(B
sin(B![]() ),c=5,
),c=5,
∴a![]() csin(B
csin(B![]() ),
),
由正弦定理可得:sinA![]() sinC
sinC![]()
![]() (sinB+cosB),
(sinB+cosB),
∴sin(B+C)=sinBcosC+cosBsinC=sinCsinB+sinCcosB,
化为:sinBcosC=sinC![]() sinB,sinB
sinB,sinB![]() 0,
0,
∴cosC=sinC,即tanC=1,C∈(0,π).
∴C![]() .
.
∴△ABC外接圆的半径R![]()
![]() .
.
如图所示,建立直角坐标系.A(![]() ,0),B(
,0),B(![]() ,0),O(0,
,0),O(0,![]() ).
).
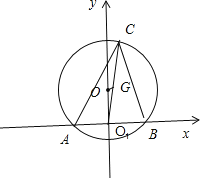
△ABC外接圆的方程为:x2![]() .
.
设C(![]() cosθ,
cosθ,![]() sinθ).θ∈(0,π)
sinθ).θ∈(0,π)
则G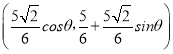 .
.
|OG|2![]() sinθ
sinθ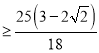 ,
,
∴|OG|的最小值为:![]() .
.
故选:D.

 阅读快车系列答案
阅读快车系列答案【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.
调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列表,并判断是否由
列表,并判断是否由![]() 的把握认为.了解阿基米德与选择文理科有关?
的把握认为.了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | p> | ||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取两人,求两人都是文科生的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;
②A品牌三种车型总销量环比增长率可能大于14.70%;
③B品牌三款车型总销量环比增长率可能为正;
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()