题目内容
经过直线x+2y-3=0与2x-y-1=0的交点且和点(0,1)的距离等于1的直线方程为 .
x-1=0
设所求直线的方程为(x+2y-3)+λ(2x-y-1)=0,即(1+2λ)x+(2-λ)y-3-λ=0,
由于点(0,1)到该直线的距离为1,
即1=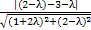 =
=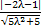 ,
,
所以|2λ+1|=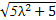 ,解得λ=2.
,解得λ=2.
故所求直线方程为
(x+2y-3)+2(2x-y-1)=0,即x-1=0.
由于点(0,1)到该直线的距离为1,
即1=
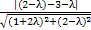 =
=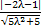 ,
,所以|2λ+1|=
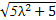 ,解得λ=2.
,解得λ=2.故所求直线方程为
(x+2y-3)+2(2x-y-1)=0,即x-1=0.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦,
的弦,
 ;
; ,求点
,求点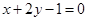 平行的直线方程是 .
平行的直线方程是 . 中,点
中,点 的坐标分别为
的坐标分别为 则
则