题目内容

假设关于某设备的使用年限ｘ和所支出的维修费用ｙ（万元），有如下的统计资料：

使用年限ｘ

2

3

4

5

6

维修费用ｙ

2.2

3.8

5.5

6.5

7.0

若由资料知ｙ对ｘ呈线性相关关系.

（1）线性回归方程的回归系数,；

（2）预报使用年限为10年时的维修费用是多少？

思路分析:因为ｙ对ｘ呈线性相关关系，所以可以用一元线性相关的方法解决问题.

（1）利用公式=-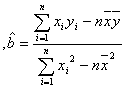.来计算回归系数.有时为了方便常制表对应写出xiyi，xi2,以利于求和.（2）获得回归直线方程后，取ｘ＝10，即可求值.

解：（1）由题意求得=4,=5,=1xi2=90,=112.3，于是

==1.23,==5-1.23×4=0.08.

（2）回归直线方程是=1.23x+0.08，当ｘ＝10（年）时，=1.23×10+0.08=12.38（万元），即估计使用10年时维修费用是12.38万元.

    深化升华 注意此处空半格知道ｘ与ｙ呈线性相关关系，就无需进行相关性检验，否则应首先进行相关性检验.如果本身两个变量不具有相关关系，或者说，它们之间相关关系不显著，即使求出了回归方程也是毫无意义的，而且估计和预测的量也是不可信的.


练习册系列答案
相关题目
假设关于某设备的使用年限x和所支出的维修费用 y（万元），有如下的统计资料：
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
若由资料可知y对x呈线性相关关系，且线性回归方程为y=a+bx，其中已知b=1.23，请估计使用年限为20年时，维修费用约为
 
．
假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料：
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
试求：
（1）对x与y进行线性相关性检验；
（2）如果y对x呈线性相关关系，求线性回归方程；（其中
a
和
b
均保留两位小数）
（3）估计使用年限为10年时，维修费用是多少万元？（保留两位小数）
（参考公式与数据：r=
n
i=1
xiyi-n
.
x
.
y
(
n
i=1
x
2
i
-n
.
x
2)(
n
i=1
y
2
i
-n
.
y
2) 
，
b
=
n
i=1
xiyi-n
.
x
.
y
n
i=1
x
2
i
-n
.
x
2
，
a
=
.
y
=
b
.
x
，
5
i=1
 
x
2
i
=90，
5
i=1
y
2
i
=140.8，
.
x
=4，
.
y
=5，
5
i=1
xiyi=1123，
79
≈8.9，
2
≈1.4，n-2=3时，r0.05=0.878）
假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料：
使用年限x 2 3 4 5 6
维修费用y 2.2 3.8 5.5 6.5 7.0
由资料知y与x呈线性相关关系．（参考数据
5
i=1
x
2
i
=90，
5
i=1
xiyi=112.3）
估计当使用年限为10年时，维修费用是
12.38
12.38
万元．
b
=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i
(xi-
.
x
)2
=
n
i=1
xiyi-n
.
x
.
y
n
i=1
x2-n
.
x
2
a
=
.
y
-b
.
x

线性回归方程：y=
b
x+
a
．
假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计数据（xi，yi）（i=1，2，3，4，5）由资料知y对x呈线性相关，并且统计的五组数据得平均值分别为
.
x
=4，
.
y
=5.4，若用五组数据得到的线性回归方程
y
=bx+a去估计，使用8年的维修费用比使用7年的维修费用多1.1万元，
（1）求回归直线方程；（2）估计使用年限为10年时，维修费用是多少？
假设关于某设备的使用年限x和所指出的维修费用y（万元），有如下统计资料：
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
若由资料可知y对x呈线性相关关系．试求：
（1）线性回归方程；
（2）估计使用年限为10年时，维修费用是多少？
（  
b
=
n
i
xiyi-n
.
x
.
y
n
i
x
2
i
-n
.
x
2
，
a
=
.
y
-
b
.
x
参考数据
5
i=1
x
2
i
=90，
5
i=1
xiyi=112.3
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网