题目内容
13.已知映射f:P→Q是从P到Q的一个函数,则P,Q的元素( )| A. | 可以是点 | B. | 可以是方程 | C. | 必须是实数 | D. | 可以是三角形 |
分析 函数是一种特殊的映射,其特殊性体现为,映射f:A→B中,集合A,B必须是非空的数集,即A,B的元素必须是实数.
解答 解:函数是一种特殊的映射,其特殊性体现为,
对于映射f:A→B,若该映射能构成函数,
则集合A,B必须是非空的数集,即A,B的元素必须是实数,
本题中,映射f:P→Q是从P到Q的一个函数,
则集合P,Q的元素必须是实数,
故选C.
点评 本题主要考查了函数与映射的概念,以及函数与映射的区别,即函数是建立在两个非空数集之间的映射,属于基础题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
1.已知函数f(x)=sin(2x+φ)(0<φ<π),若将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位后所得图象对应的函数为偶函数,则实数φ=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
18.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | f(x)=$\frac{2}{x}$ | B. | f(x)=log2x | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=-x2+2 |
3.已知函数y=f(x),x∈R,f(0)≠0,且满足f(x1)+f(x2)=2f($\frac{{x}_{1}+{x}_{2}}{2}$)f($\frac{{x}_{1}-{x}_{2}}{2}$),则函数f(x)的奇偶性为( )
| A. | 是奇函数而不是偶函数 | B. | 是偶函数而不是奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数也不是偶函数 |
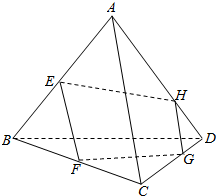 如图,ABCD为空间四边形,点E,F分别是AB,BC的中点,点G,H分别在CD,AD上,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$CD.
如图,ABCD为空间四边形,点E,F分别是AB,BC的中点,点G,H分别在CD,AD上,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$CD.