题目内容
甲、乙、丙三人组成一组,参加一个闯关游戏团体赛,三人各自独立闯关,其中甲闯关成功的概率为 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为 .每人闯关成功记2分,不成功为0分,三人得分之和记为小组团体总分.
.每人闯关成功记2分,不成功为0分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)记团体总分为随机变量§,求§的概率分布列.
解:(1)设乙闯关成功的概率为P1,丙闯关成功的概率为P2.…(1分)
因为乙丙独立闯关,根据独立事件同时发生的概率公式得: …(3分)
…(3分)
解得P1= ,P2=
,P2= …(4分)
…(4分)
答:乙闯关成功的概率为 ,丙闯关成功的概率为
,丙闯关成功的概率为 .
.
(2)团体总分为(4分),即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为(4分)”为事件A,则P(A)=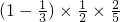 +
+ +
+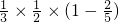 =
=
答:团体总分为(4分)的概率为 .…(8分)
.…(8分)
(3)§=0,2,4,6 (1分)
P(§=0)=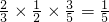
P(§=2)=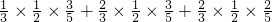 =
=
由(2)P(§=4)=
P(§=6)=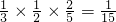 …(10分)
…(10分)
§的分布列为
…(12分)
分析:(1)设乙闯关成功的概率为P1,丙闯关成功的概率为P2,根据甲闯关成功的概率为 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为 ,建立方程组,即可求得乙、丙各自闯关成功的概率;
,建立方程组,即可求得乙、丙各自闯关成功的概率;
(2)团体总分为(4分),即甲、乙、丙三人中恰有2人过关,而另外一人没过关,由此可求概率;
(3)确定§的取值,求出相应的概率,即可得到§的概率分布列.
点评:本题考查互斥事件,考查离散型随机事件的分布列,确定变量的取值,计算相应的概率是关键.
因为乙丙独立闯关,根据独立事件同时发生的概率公式得:
 …(3分)
…(3分)解得P1=
 ,P2=
,P2= …(4分)
…(4分)答:乙闯关成功的概率为
 ,丙闯关成功的概率为
,丙闯关成功的概率为 .
.(2)团体总分为(4分),即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为(4分)”为事件A,则P(A)=
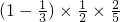 +
+ +
+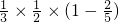 =
=
答:团体总分为(4分)的概率为
 .…(8分)
.…(8分)(3)§=0,2,4,6 (1分)
P(§=0)=
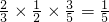
P(§=2)=
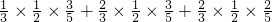 =
=
由(2)P(§=4)=

P(§=6)=
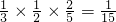 …(10分)
…(10分)§的分布列为
| § | 0 | 2 | 4 | 6 |
| P |  |  |  |  |
分析:(1)设乙闯关成功的概率为P1,丙闯关成功的概率为P2,根据甲闯关成功的概率为
 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为 ,建立方程组,即可求得乙、丙各自闯关成功的概率;
,建立方程组,即可求得乙、丙各自闯关成功的概率;(2)团体总分为(4分),即甲、乙、丙三人中恰有2人过关,而另外一人没过关,由此可求概率;
(3)确定§的取值,求出相应的概率,即可得到§的概率分布列.
点评:本题考查互斥事件,考查离散型随机事件的分布列,确定变量的取值,计算相应的概率是关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为 ,每人闯关成功得2分,三人得分之和记为小组团体总分.
,每人闯关成功得2分,三人得分之和记为小组团体总分.
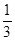 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为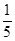 ,每人闯关成功得2分,三人得分之和记为小组团体总分.
,每人闯关成功得2分,三人得分之和记为小组团体总分.