题目内容
甲、乙、丙三人组成一组，参加一个闯关游戏团体赛．三人各自独立闯关，其中甲闯关成功的概率为| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 5 |
（I）求乙、丙各自闯关成功的概率；
（II）求团体总分为4分的概率；
（III）若团体总分不小于4分，则小组可参加复赛．求该小组参加复赛的概率．
分析：（I）由题意知三人各自独立闯关，其中甲闯关成功的概率为
，甲、乙都闯关成功的概率为
，乙、丙都闯关成功的概率为
设出乙闯关成功的概率和丙闯关成功的概率，列出两组闯关的概率的关系式，解方程，得到结果．
（II）团体总分为4分，即甲、乙、丙三人中恰有2人过关，而另外一人没过关，写出概率，把所有的概率的值相加，得到结果．
（III）团体总分不小于4分，即团体总分为4分或6分，在上一问已经做出总分是4分的概率，只要再做出总分是6分的概率即可，团体总分为6分，即3人都闯关成功，得到结果．
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 5 |
设出乙闯关成功的概率和丙闯关成功的概率，列出两组闯关的概率的关系式，解方程，得到结果．
（II）团体总分为4分，即甲、乙、丙三人中恰有2人过关，而另外一人没过关，写出概率，把所有的概率的值相加，得到结果．
（III）团体总分不小于4分，即团体总分为4分或6分，在上一问已经做出总分是4分的概率，只要再做出总分是6分的概率即可，团体总分为6分，即3人都闯关成功，得到结果．
解答：解：（I）三人各自独立闯关，其中甲闯关成功的概率为
，
甲、乙都闯关成功的概率为
，乙、丙都闯关成功的概率为
设乙闯关成功的概率为P1，丙闯关成功的概率为P2
∵乙丙独立闯关，
根据独立事件同时发生的概率公式得：
解得P1=
，P2=
．
即乙闯关成功的概率为
，丙闯关成功的概率为
．
（II）团体总分为4分，即甲、乙、丙三人中恰有2人过关，而另外一人没过关．
设“团体总分为4分”为事件A，
则P(A)=(1-
)×
×
+
×(1-
)×
+
×
×(1-
)=
．
即团体总分为4分的概率为
．
（III）团体总分不小于4分，即团体总分为4分或6分，
设“团体总分不小于4分”为事件B，
由（II）知团体总分为4分的概率为
，
团体总分为6分，即3人都闯关成功的概率为
×
×
=
．
所以参加复赛的概率为P（B）=
+
=
．
即该小组参加复赛的概率为
．
| 1 |
| 3 |
甲、乙都闯关成功的概率为
| 1 |
| 6 |
| 1 |
| 5 |
设乙闯关成功的概率为P1，丙闯关成功的概率为P2
∵乙丙独立闯关，
根据独立事件同时发生的概率公式得：
|
解得P1=
| 1 |
| 2 |
| 2 |
| 5 |
即乙闯关成功的概率为
| 1 |
| 2 |
| 2 |
| 5 |
（II）团体总分为4分，即甲、乙、丙三人中恰有2人过关，而另外一人没过关．
设“团体总分为4分”为事件A，
则P(A)=(1-
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
| 3 |
| 10 |
即团体总分为4分的概率为
| 3 |
| 10 |
（III）团体总分不小于4分，即团体总分为4分或6分，
设“团体总分不小于4分”为事件B，
由（II）知团体总分为4分的概率为
| 3 |
| 10 |
团体总分为6分，即3人都闯关成功的概率为
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 15 |
所以参加复赛的概率为P（B）=
| 3 |
| 10 |
| 1 |
| 15 |
| 11 |
| 30 |
即该小组参加复赛的概率为
| 11 |
| 30 |
点评：本题考查独立重复试验，考查相互独立事件同时发生的概率，是一个基础题目，题干比较长注意首先要审题，这是解题的关键．
练习册系列答案
综合自测系列答案
相关题目
，甲、乙都闯关成功的概率为
，乙、丙都闯关成功的概率为
.每人闯关成功记2分，三人得分之和记为小组团体总分.
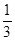，甲、乙都闯关成功的概率为
，乙、丙都闯关成功的概率为
，每人闯关成功得2分，三人得分之和记为小组团体总分.
，甲、乙都闯关成功的概率为
，乙、丙都闯关成功的概率为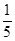
，每人闯关成功得2分，三人得分之和记为小组团体总分.