题目内容
如图,在长方体ABCD-A1B1C1D1中,AD=AA1,AB=2,点E在棱AB上.
(1)证明:D1E⊥A1D;
(2)当E点为线段AB的中点时,求异面直线D1E与AC所成角的余弦值;
(3)试问E点在何处时,平面D1EC与平面AA1D1D所成二面角的平面角的余弦值为
.

(1)证明:D1E⊥A1D;
(2)当E点为线段AB的中点时,求异面直线D1E与AC所成角的余弦值;
(3)试问E点在何处时,平面D1EC与平面AA1D1D所成二面角的平面角的余弦值为
| ||
| 6 |

以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,
设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A=(1,0,0),C(0,2,0).…(2分)
(1)因为
=(1,0,1),
=(1,x,-1)
∴
•
=1+0-1=0,所以D1E⊥A1D;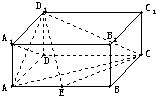
(2)因为E为AB中点,则E(1,1,0),
从而
=(1,1,-1),
=(-1,2,0),
设AC与D1E所成的角为θ
则 cosθ=
=
=
…(9分)
(3)设平面D1EC的法向量为
=(a,b,c),
∵
=(1,x-2,0),
=(0,2,-1),
=(0,0,1)
由
,有
,
令b=1,从而c=2,a=2-x
∴
=(2-x,1,2),…..(12分)
由题意,cos θ=
=
=
∴x=3(不合题意,舍去),或x=1.
∴当AE=1,即E为线段AB的中点时,平面D1EC与平面AA1D1D所成二面角的平面角的余弦值为
.
设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A=(1,0,0),C(0,2,0).…(2分)
(1)因为
| DA1 |
| D1E |
∴
| DA1 |
| D1E |

(2)因为E为AB中点,则E(1,1,0),
从而
| D1E |
| AC |
设AC与D1E所成的角为θ
则 cosθ=
|
| ||||
|
|
| |-1+2+0| | ||||
|
| ||
| 15 |
(3)设平面D1EC的法向量为
| n |
∵
| CE |
| D1C |
| DD1 |
由
|
|
令b=1,从而c=2,a=2-x
∴
| n |
由题意,cos θ=
| ||||
|
|
| 2 | ||
2
|
| ||
| 6 |
∴x=3(不合题意,舍去),或x=1.
∴当AE=1,即E为线段AB的中点时,平面D1EC与平面AA1D1D所成二面角的平面角的余弦值为
| ||
| 6 |

练习册系列答案
相关题目

 且
且 ,给出下列命题:
,给出下列命题: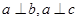 则
则 ②
②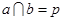 则
则
 ④若
④若 则
则