题目内容
已知二次函数g(x)对任意实数x不等式x-1≤g(x)≤x2-x恒成立,且g(-1)=0,令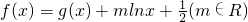 .
.
(I)求g(x)的表达式;
(II)若?x>0使f(x)≤0成立,求实数m的取值范围;
(III)设1<m≤e,H(x)=f(x)-(m+1)x,证明:对?x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1.
解(I)设g(x)=ax2+bx+c(a≠0),
由题意令x=1得0≤g(1)≤0∴g(1)=0,
∴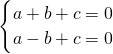 得b=0,a+c=0,
得b=0,a+c=0,
∵x-1≤g(x)≤x2-x对?x∈R恒成立,
∴ax2-a≥x-1和ax2-a≤x2-x恒成立,
得 ,
,
∴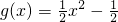 .
.
(II)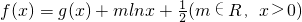 =
=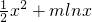 ,
,

当m>0时,f(x)的值域为R
当m=0时,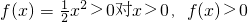 恒成立
恒成立
当m<0时,令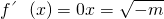
这时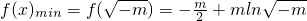
若?x>0使f(x)≤0成立则只须f(x)min≤0即m≤-e,
综上所述,实数m的取值范围(-∞,-e)∪(0,+∞).
(III)∵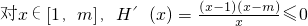 ,所以H(x)在[1,m]单减
,所以H(x)在[1,m]单减
于是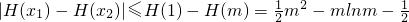 ,
,
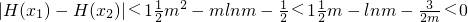 ,
,
记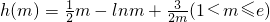 ,则
,则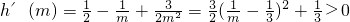
所以函数h(m)在[1,e]是单增函数
所以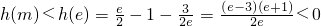
故命题成立.
分析:(I)直接设出g(x)的表达式,利用不等式x-1≤g(x)≤x2-x恒成立,可得g(1)=0与g(-1)=0相结合可得b=0,a+c=0;再代入利用不等式x-1≤g(x)≤x2-x恒成立求出a即可.
(II)先求出函数f(x)的表达式,在对实数m分情况求出对应函数f(x)的值域,让实数m与函数f(x)的最小值比较即可求实数m的取值范围;
(III)先求出函数H(x)在[1,m]单减,进而得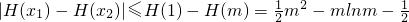 ,转化为求
,转化为求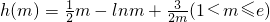 的最大值问题即可.
的最大值问题即可.
点评:本题主要考查函数恒成立问题以及函数解析式的求法,是对函数以及导函数知识的综合考查,是有难度的题.
由题意令x=1得0≤g(1)≤0∴g(1)=0,
∴
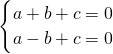 得b=0,a+c=0,
得b=0,a+c=0,∵x-1≤g(x)≤x2-x对?x∈R恒成立,
∴ax2-a≥x-1和ax2-a≤x2-x恒成立,
得
 ,
,∴
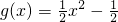 .
.(II)
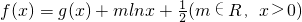 =
=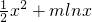 ,
,
当m>0时,f(x)的值域为R
当m=0时,
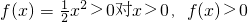 恒成立
恒成立当m<0时,令
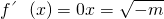
| x | 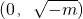 | 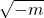 | 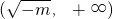 |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小 | ↗ |
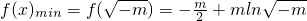
若?x>0使f(x)≤0成立则只须f(x)min≤0即m≤-e,
综上所述,实数m的取值范围(-∞,-e)∪(0,+∞).
(III)∵
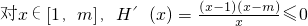 ,所以H(x)在[1,m]单减
,所以H(x)在[1,m]单减于是
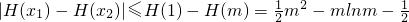 ,
,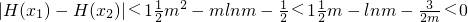 ,
,记
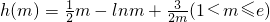 ,则
,则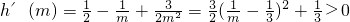
所以函数h(m)在[1,e]是单增函数
所以
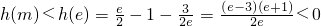
故命题成立.
分析:(I)直接设出g(x)的表达式,利用不等式x-1≤g(x)≤x2-x恒成立,可得g(1)=0与g(-1)=0相结合可得b=0,a+c=0;再代入利用不等式x-1≤g(x)≤x2-x恒成立求出a即可.
(II)先求出函数f(x)的表达式,在对实数m分情况求出对应函数f(x)的值域,让实数m与函数f(x)的最小值比较即可求实数m的取值范围;
(III)先求出函数H(x)在[1,m]单减,进而得
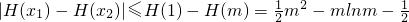 ,转化为求
,转化为求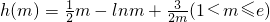 的最大值问题即可.
的最大值问题即可.点评:本题主要考查函数恒成立问题以及函数解析式的求法,是对函数以及导函数知识的综合考查,是有难度的题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目