题目内容
【题目】在平面直角坐标系中,设点![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示a、b中的较大数)为
表示a、b中的较大数)为![]() 、
、![]() 两点的“切比雪夫距离”.
两点的“切比雪夫距离”.
(1)若![]() ,Q为直线
,Q为直线![]() 上动点,求P、Q两点“切比雪夫距离”的最小值;
上动点,求P、Q两点“切比雪夫距离”的最小值;
(2)定点![]() ,动点
,动点![]() 满足
满足![]()
![]() ,请求出P点所在的曲线所围成图形的面积.
,请求出P点所在的曲线所围成图形的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设![]() ,可得
,可得![]() ,讨论
,讨论![]() 的大小,可得距离
的大小,可得距离![]() ,再结合函数的性质求最小值即可;
,再结合函数的性质求最小值即可;
(2)运用分段函数的形式求得![]() ,分析各段与不等式表示的平面区域的图形,即可求得面积.
,分析各段与不等式表示的平面区域的图形,即可求得面积.
解:(1)设![]() ,可得
,可得![]() ,
,
由![]() ,解得
,解得![]() ,即有
,即有![]() ,则当
,则当![]() 时,
时,![]() 取最小值
取最小值![]() ;
;
由![]() ,解得
,解得![]() 或
或![]() ,即有
,即有![]() ,即
,即![]() ,
,
综上可得:P、Q两点“切比雪夫距离”的最小值为![]() ;
;
(2)由题意可得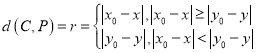 ,
,
当![]() ,即有
,即有![]() ,
,
则围成的图形为关于点![]() 对称的三角形区域,
对称的三角形区域,
当![]() ,即有
,即有![]() ,
,
则围成的图形为关于点![]() 对称的三角形区域,
对称的三角形区域,
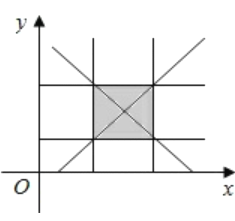
综上可得,P点所在的曲线所围成图形为边长为![]() 的正方形区域,则该区域面积为
的正方形区域,则该区域面积为![]() ,
,
故P点所在的曲线所围成图形的面积为![]() .
.

练习册系列答案
相关题目