题目内容
已知三棱锥S-ABC中，底面ABC为边长等于2的等边三角形，SA垂直于底面ABC，SA=2
，D为SA的中点，那么直线BD与直线SC所成角的大小为
| 2 |
45°
45°
．分析：先利用三角形中位线定理证明DE∥SC，从而找到异面直线所成的角的平面角，再利用线面垂直的判定和性质证明此角所在三角形为直角三角形，最后在三角形中计算此角即可
解答：解：如图：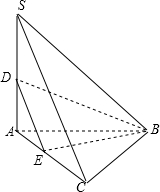
取AC中点E，连接BE，DE
∴DE∥SC
∴∠BDE就是异面直线BD与SC所成角或其补角
∵SA⊥底面ABC，BE?底面ABC
∴BE⊥SA，而在正三角形ABC中，BE⊥AC，SA∩AC=A
∴BE⊥平面SAC，DE?平面SAC
∴BE⊥DE
在Rt△DEB中，BE=2×sin60°=
DE=
SC=
=
∴∠BDE=45°
故答案为45°
取AC中点E，连接BE，DE∴DE∥SC
∴∠BDE就是异面直线BD与SC所成角或其补角
∵SA⊥底面ABC，BE?底面ABC
∴BE⊥SA，而在正三角形ABC中，BE⊥AC，SA∩AC=A
∴BE⊥平面SAC，DE?平面SAC
∴BE⊥DE
在Rt△DEB中，BE=2×sin60°=
| 3 |
DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 8+4 |
| 3 |
∴∠BDE=45°
故答案为45°
点评：本题考查了异面直线所成的角的作法，证法，求法，将空间问题转化为平面问题的思想方法
练习册系列答案
相关题目