题目内容
(本小题满分12分)
函数f(x) =  sinωxcosωx +
sin2ωx +
sinωxcosωx +
sin2ωx +  ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为
 .
.
(Ⅰ)求ω的值;
(Ⅱ) 若A为△ABC的内角,且f  =
=  ,求A的值.
,求A的值.
【答案】
(Ⅰ)f(x) = sin + 1;(2)A =
+ 1;(2)A =  .
.
【解析】
试题分析:(1)将f(x)解析式第一项利用二倍角的余弦函数公式化简,第二项第二个因式利用诱导公式变形,再利用二倍角的正弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,由y=f(x)的图象相邻两条对称轴之间的距离为  ,得到f(x)的周期为π,利用周期公式求出ω的值.确定出f(x)的解析式.
,得到f(x)的周期为π,利用周期公式求出ω的值.确定出f(x)的解析式.
(2)由f  = sin
= sin + 1 =
+ 1 =
 ∴sin
∴sin =
=  ,再结合A∈(0,π),可得A =
,再结合A∈(0,π),可得A =  .
.
(Ⅰ)f(x) =  sin2ωx +
sin2ωx +  +
+ 
=
 sin2ωx −
sin2ωx −  cos2ωx + 1 =
sin
cos2ωx + 1 =
sin + 1
+ 1
∵函数图像的相邻两条对称轴之间的距离为
 ,∴最小正周期T = π
,∴最小正周期T = π
∴ = π,ω = 1.
= π,ω = 1.
∴f(x) = sin + 1
+ 1
(2) ∵f  = sin
= sin + 1 =
+ 1 =
 ∴sin
∴sin =
= 
∵ A∈(0,π) ∴ − 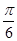 < A −
< A − 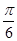 <
< 
∴ A − 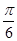 =
= 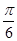 ,故A =
,故A =  .
.
考点:考查了三角诱导公式及三角函数的图像及性质,给值求角等知识.
点评:掌握三角诱导公式是化简的基础,再求解的过程中要注意角的范围,本小题同时还考查了三角函数的图像及三角函数的性质,属于容易题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目