题目内容
| |||||||||||||||
(x∈R)，
，(n＝1，2，3，4，…，100)，求数列{an}的前100项和S100
，(m∈N+，n＝1，2，3，4，…，m)，且数列{an}的前m项和为Sm，又设数列满足：b1＝
，bn+1＝bn2＋bn，且
，若Sm满足对任意不小于2的正整数n，都有Sm＜Tn恒成立，试求m的最大值？
答案：
解析：
解析：
(1) |
解： |
(2) |
解：
故而 |
(3) |
解：由(2)式的方法，得出
所以数列 故而 又因为 所以 从而有 |
……………………(4分)
(1)
(2)
…………………………………………(4分)
…………………………………………(5分)
……………………(1分)
，
为递增的正数数列
的最小值为
……………………(2分)
，所以
……………………(3分)
恒成立即只要
即可
练习册系列答案
名校课堂系列答案
相关题目
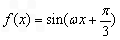(x∈R,
)的图象如图，P是图象的最高点，Q是图象的最低点．且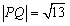
．
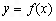的解析式；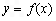
图象向右平移1个单位后得到函数
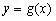的图象，当
时，求函数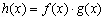
的最大值．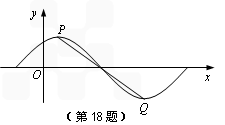
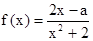(x∈R)在区间[-1,1]上是增函数
的两实数根为x1、x2,试问:是否存在实数m,使得不等式
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由? 
(x∈R)在区间[-1,1]上是增函数（Ⅰ）求实数a的值所组成的集合A（Ⅱ）设关于x的方程
的两实数根为x1、x2.
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由? 
(x∈R)在区间[-1,1]上是增函数.
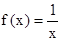的两实数根为x1、x2,试问:是否存在实数m,使得不等式
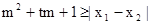对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由? 
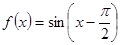(x∈R),下面结论错误的是 （ ）
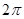； B.函数f(x)在区间
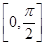是增函数；