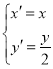题目内容
【题目】已知函数![]() 在
在![]() 处取得极小值.
处取得极小值.
(1)求实数![]() 的值;
的值;
(2)若函数![]() 存在极大值与极小值,且函数
存在极大值与极小值,且函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.(参考数据:
的取值范围.(参考数据:![]() ,
,![]() )
)
【答案】(1)![]() 或
或![]() (2)
(2)![]()
【解析】
(1)根据极值的定义,求出![]() 或
或![]() ,再对
,再对![]() 的两种取值分别进行验证;
的两种取值分别进行验证;
(2)由第(1)问先确定![]() ,得到
,得到![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性,即函数
的单调性,即函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,再结合零点存在定理的条件,得到参数
上单调递减,再结合零点存在定理的条件,得到参数![]() 的取值范围.
的取值范围.
解:(1)由题意得![]() .
.
因为函数![]() 在
在![]() 处取得极小值,
处取得极小值,
依题意知![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,若
,若![]() ,
,![]() ,则函数
,则函数![]() 单调递减,
单调递减,
若![]() ,
,![]() ,则函数
,则函数![]() 单调递增,
单调递增,
所以,当![]() 时,
时,![]() 取得极小值,无极大值,符合题意.
取得极小值,无极大值,符合题意.
当![]() 时,
时,![]() ,若
,若![]() 或
或![]() ,
,![]() ,则函数
,则函数![]() 单调递增;
单调递增;
若![]() ,
,![]() ,则函数
,则函数![]() 单调递减,所以函数
单调递减,所以函数![]() 在
在![]() 处取得极小值,
处取得极小值,![]() 处取得极大值,符合题意,
处取得极大值,符合题意,
综上,实数![]() 或
或![]() .
.
(2)因为函数![]() 存在极大值与极小值,所以由(1)知,
存在极大值与极小值,所以由(1)知,![]() .
.
所以![]() ,
,![]() .
.
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,令
时,令![]() ,则
,则![]() ,所以当
,所以当![]() 或
或![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
因为![]() ,
,
![]() ,所以当
,所以当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减.
上单调递减.
因为函数![]() 在
在![]() 上有两个零点,所以
上有两个零点,所以![]() ,所以
,所以![]() .
.
取![]() ,
, ;
;
取![]() ,
,![]() ,
,
所以,实数![]() 的取值范围是
的取值范围是![]() .
.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】至2018年底,我国发明专利申请量已经连续8年位居世界首位,下表是我国2012年至2018年发明专利申请量以及相关数据.
总计 | ||||||||
年代代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 28 |
申请量 | 65 | 82 | 92 | 110 | 133 | 138 | 154 | 774 |
| 65 | 164 | 276 | 440 | 665 | 828 | 1078 | 3516 |
注:年代代码1~7分别表示2012~2018.
(1)可以看出申请量每年都在增加,请问这几年中那一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
参考公式: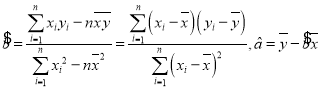 .
.
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
甲公司某员工A | 乙公司某员工B | |||||||||||||
3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
0 | 1 | 4 | 4 | 2 | 2 | 2 | ||||||||
每名快递员完成一件货物投递可获得的劳务费情况如下:
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.