题目内容
已知函数![]() 的定义域为
的定义域为![]() ,且对任意
,且对任意![]() ,都有
,都有![]() ,且当
,且当![]() 时,
时,![]() 恒成立,
恒成立,
证明:(1)函数![]() 是
是![]() 上的减函数;
上的减函数;
(2)函数![]() 是奇函数。
是奇函数。
证明见解析
解析:
证明:(1)设![]() ,则
,则![]() ,而
,而![]()
∴![]()
∴函数![]() 是
是![]() 上的减函数;
上的减函数;
(2)由![]() 得
得![]()
即![]() ,而
,而![]()
∴![]() ,即函数
,即函数![]() 是奇函数。
是奇函数。

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为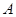 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.