题目内容
已知函数f(x)=ax(x-1)2+1,(x∈R)和函数g(x)=(2-a)x3+3ax2-ax,(x∈R)
(Ⅰ)令h(x)=f(x)+g(x),若函数h(x)在[1,+∞)上存在单调递减区间,求实数a的取值范围.
(Ⅱ)当a<0时,若F(x)=f(x)+a有极大值-7,求实数a的值.
(Ⅰ)令h(x)=f(x)+g(x),若函数h(x)在[1,+∞)上存在单调递减区间,求实数a的取值范围.
(Ⅱ)当a<0时,若F(x)=f(x)+a有极大值-7,求实数a的值.
分析:(Ⅰ)对函数h(x)求导,利用函数h(x)在[1,+∞)上存在单调递减区间,则说明h'(x)<0有解.
(Ⅱ)利用函数F(x)=f(x)+a有极大值-7,可求实数a的值.
(Ⅱ)利用函数F(x)=f(x)+a有极大值-7,可求实数a的值.
解答: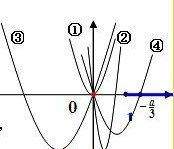 解:(Ⅰ)∵h(x)=f(x)+g(x)=2x3+ax2+1.
解:(Ⅰ)∵h(x)=f(x)+g(x)=2x3+ax2+1.
∴h'(x)=6x2+2ax,…(2分)
由题意要使函数h(x)在[1,+∞)上存在单调递减区间,h'(x)<0在[1,+∞)上有解.
∵h'(x)=6x2+2ax=0,解得x=0或x=-
.
由图象可知当-
>1(图④正确),解得a<-3.
(Ⅱ)F(x)=f(x)+a=ax(x-1)2+a+1,
所以F'(x)=a(3x2-4x+1),令F'(x)=0,得3x2-4x+1=0,解得x=1或x=
.
列表:
∴F(x)在x=1处取得极大值-7,即a+1=-7,解得a=-8.
 解:(Ⅰ)∵h(x)=f(x)+g(x)=2x3+ax2+1.
解:(Ⅰ)∵h(x)=f(x)+g(x)=2x3+ax2+1.∴h'(x)=6x2+2ax,…(2分)
由题意要使函数h(x)在[1,+∞)上存在单调递减区间,h'(x)<0在[1,+∞)上有解.
∵h'(x)=6x2+2ax=0,解得x=0或x=-
| a |
| 3 |
由图象可知当-
| a |
| 3 |
(Ⅱ)F(x)=f(x)+a=ax(x-1)2+a+1,
所以F'(x)=a(3x2-4x+1),令F'(x)=0,得3x2-4x+1=0,解得x=1或x=
| 1 |
| 3 |
列表:
| x | (-∞,
|
|
(
|
1 | (1,+∞) | ||||||
| F'(x) | - | + | - | ||||||||
| F(x) | 递减 | 极小值 | 递增 | 极大值a+1 | 递减 |
点评:本题主要考查了利用导数研究函数的单调性和极值的问题,属于常考题型要求熟练掌握.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目