题目内容
17.(1)已知x>2,求$y=x+\frac{3}{x-2}$的最小值;(2)已知$0<x<\frac{1}{2}$,求y=3x(1-2x)的最大值.
分析 (1)由题意可得x-2>0,变形可得$y=x+\frac{3}{x-2}$=x-2+$\frac{3}{x-2}$+2,应用基本不等式可得;
(2)由题意可得0<1-2x<1,变形可得y=3x(1-2x)=$\frac{3}{2}$•2x(1-2x),由基本不等式可得.
解答 解:(1)∵x>2,∴x-2>0,
∴$y=x+\frac{3}{x-2}$=x-2+$\frac{3}{x-2}$+2
≥2$\sqrt{(x-2)•\frac{3}{x-2}}$+2=2$\sqrt{3}$+2
当且仅当x-2=$\frac{3}{x-2}$即x=2+$\sqrt{3}$时等号成立.
∴当x=2+$\sqrt{3}$时函数取最小值2$\sqrt{3}$+2;
(2)∵$0<x<\frac{1}{2}$,∴0<1-2x<1
∴y=3x(1-2x)=$\frac{3}{2}$•2x(1-2x)
≤$\frac{3}{2}$•$(\frac{2x+1-2x}{2})^{2}$=$\frac{3}{8}$
当且仅当2x=(1-2x)即x=$\frac{1}{4}$时等号成立.
∴当x=$\frac{1}{4}$时,函数取最大值$\frac{3}{8}$.
点评 本题考查基本不等式求最值,变形凑出可用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
7.函数$f(x)=\frac{1}{{\sqrt{1-x}}}$的定义域是( )
| A. | [1,+∞) | B. | (-∞,1) | C. | (-∞,1] | D. | (1,+∞) |
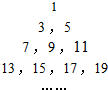 将正奇数排成如图所示的三角形数表:
将正奇数排成如图所示的三角形数表: