题目内容
已知点(1, 2)在函数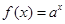 (
(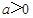 且
且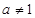 )的图象上,等比数列
)的图象上,等比数列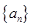 的前
的前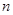 项和为
项和为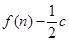 ,数列
,数列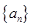
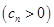 的首项为c,且其前
的首项为c,且其前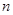 项和
项和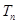 满足 2
满足 2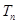 =
=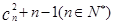 .
.
(1)求数列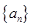 和
和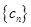 的通项公式;
的通项公式;
(2)若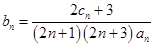 ,求数列
,求数列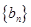 的前
的前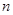 项和
项和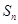 .
.
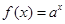 (
(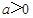 且
且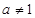 )的图象上,等比数列
)的图象上,等比数列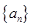 的前
的前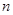 项和为
项和为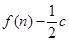 ,数列
,数列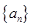
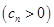 的首项为c,且其前
的首项为c,且其前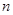 项和
项和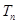 满足 2
满足 2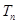 =
=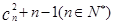 .
.(1)求数列
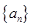 和
和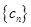 的通项公式;
的通项公式;(2)若
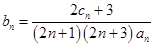 ,求数列
,求数列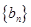 的前
的前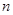 项和
项和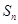 .
. (1)
(2)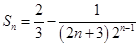

(2)
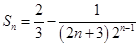
(1)因为点(1, 2)是函数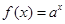 (
(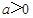 且
且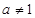 )的图象上,据此可求出
)的图象上,据此可求出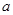 ,因而确定
,因而确定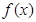 .
.
∵数列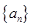 的前
的前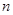 项和为
项和为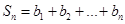 ,所以可得
,所以可得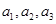 ,根据
,根据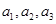 成等比数列,可建立关于c的方程求出c值.进而得到公比q=2.所以
成等比数列,可建立关于c的方程求出c值.进而得到公比q=2.所以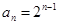 .
.
再根据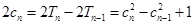 可得到
可得到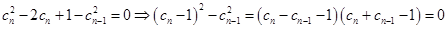 ,
,
因为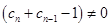 ,可得
,可得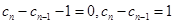 ,进而得到
,进而得到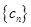 的通项公式.
的通项公式.
∵点(1, 2)是函数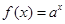 (
(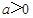 且
且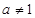 )的图象上,
)的图象上,
∴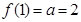 ,∴
,∴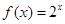 …………………… 1分
…………………… 1分
∵数列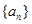 的前
的前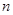 项和为
项和为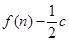 ,∴
,∴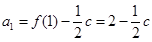 ,
,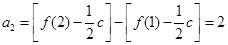 ,
,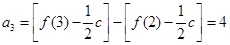
又数列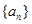 是等比数列,
是等比数列,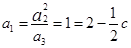 ,∴
,∴ ,公比
,公比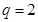 ,……… 4分
,……… 4分
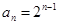 ………………………………5分
………………………………5分
当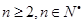 ,
,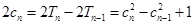 ,
,
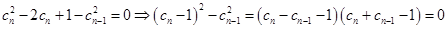 ,
,
∵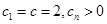 ,∴
,∴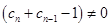 ,∴
,∴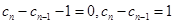 ……… 7分
……… 7分
所以数列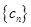 是首项是2,公差是1的等差数列,其通项公式为:
是首项是2,公差是1的等差数列,其通项公式为:
………………………………8分
(2)解本小题的关键是先得到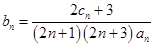
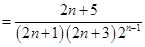 .
.
然后转化成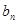
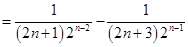 ,再采用裂项求和的方法求和即可.
,再采用裂项求和的方法求和即可.
解:由(1),得
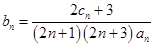
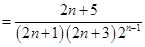 .………………………9分
.………………………9分
所以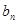
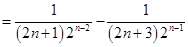 .………11分
.………11分
所以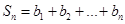
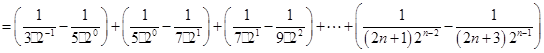 .
.
 ……………………………13分
……………………………13分
故数列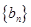 的前
的前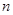 项和
项和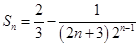 .…………………………14分
.…………………………14分
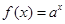 (
(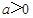 且
且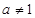 )的图象上,据此可求出
)的图象上,据此可求出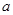 ,因而确定
,因而确定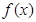 .
.∵数列
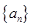 的前
的前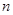 项和为
项和为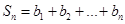 ,所以可得
,所以可得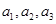 ,根据
,根据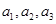 成等比数列,可建立关于c的方程求出c值.进而得到公比q=2.所以
成等比数列,可建立关于c的方程求出c值.进而得到公比q=2.所以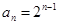 .
.再根据
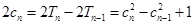 可得到
可得到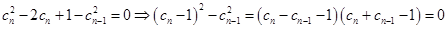 ,
,因为
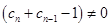 ,可得
,可得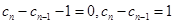 ,进而得到
,进而得到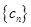 的通项公式.
的通项公式.∵点(1, 2)是函数
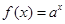 (
(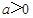 且
且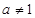 )的图象上,
)的图象上,∴
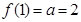 ,∴
,∴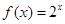 …………………… 1分
…………………… 1分∵数列
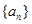 的前
的前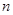 项和为
项和为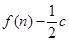 ,∴
,∴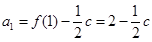 ,
,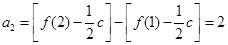 ,
,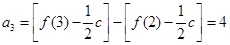
又数列
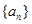 是等比数列,
是等比数列,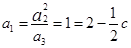 ,∴
,∴ ,公比
,公比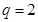 ,……… 4分
,……… 4分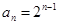 ………………………………5分
………………………………5分当
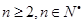 ,
,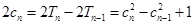 ,
,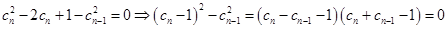 ,
,∵
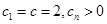 ,∴
,∴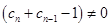 ,∴
,∴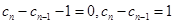 ……… 7分
……… 7分所以数列
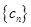 是首项是2,公差是1的等差数列,其通项公式为:
是首项是2,公差是1的等差数列,其通项公式为:
………………………………8分
(2)解本小题的关键是先得到
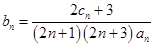
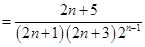 .
.然后转化成
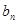
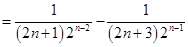 ,再采用裂项求和的方法求和即可.
,再采用裂项求和的方法求和即可.解:由(1),得
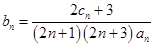
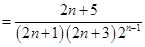 .………………………9分
.………………………9分所以
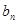
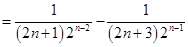 .………11分
.………11分所以
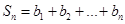
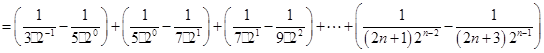 .
. ……………………………13分
……………………………13分故数列
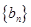 的前
的前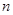 项和
项和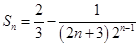 .…………………………14分
.…………………………14分
练习册系列答案
相关题目
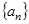 的前
的前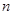 项和
项和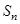 满足
满足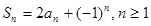 .
.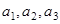 ;
;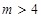 ,有
,有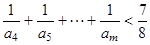 .
. 的前n项和为Sn,若
的前n项和为Sn,若 ,则这个数列一定是( )
,则这个数列一定是( )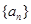 是等比数列,
是等比数列,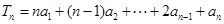 ,已知
,已知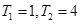 , (1)求数列
, (1)求数列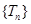 的通项公式。
的通项公式。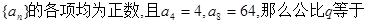 ( )
( ) 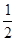
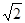
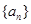 为等比数列,数列
为等比数列,数列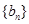 满足
满足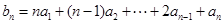 ,
,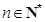 ,已知
,已知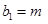 ,
,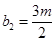 ,其中
,其中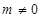 .
.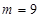 时,求
时,求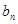 ;
;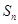 为数列
为数列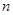 项和,若对于任意的正整数
项和,若对于任意的正整数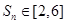 ,求实数
,求实数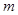 的取值范围.
的取值范围. 前
前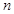 项和为
项和为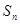 ,若
,若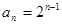 ,则
,则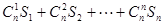 等于( )
等于( )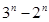
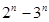

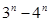
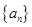 的前
的前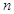 项为
项为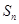 ,
,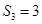 ,
,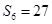 ,则此等比数列的公比
,则此等比数列的公比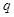 等于______
等于______