题目内容
将函数g(x)=sin2x的图象上各点的横坐标向右平移 个单位后,再把横坐标伸长为原来的2倍(纵坐标不变),得到函数y=f(x)的图象.
个单位后,再把横坐标伸长为原来的2倍(纵坐标不变),得到函数y=f(x)的图象.(1)求函数f(x)的解析式和初相;
(2)若A为三角形的内角,且f(a)=
 ,求g(
,求g( )的值.
)的值.
【答案】分析:(1)根据函数图象的平移变换法则及周期变换法则,我们易根据已知中将函数g(x)=sin2x的图象上各点的横坐标向右平移 个单位后,再把横坐标伸长为原来的2倍(纵坐标不变),得到函数y=f(x)的图象.求出函数的解析式,进而求出其初相.
个单位后,再把横坐标伸长为原来的2倍(纵坐标不变),得到函数y=f(x)的图象.求出函数的解析式,进而求出其初相.
(2)根据A为三角形的内角,且f(a)= ,我们易根据三角函数同角三角函数关系式,及两角和的正切公式求出A的正弦值,进而得到答案.
,我们易根据三角函数同角三角函数关系式,及两角和的正切公式求出A的正弦值,进而得到答案.
解答:解:(1)将函数g(x)=sin2x的图象上各点的横坐标向右平移 个单位后,
个单位后,
再把横坐标伸长为原来的2倍(纵坐标不变),
可以得到函数y=f(x)的图象
∴f(x)=sin(x-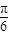 )
)
∴函数的初相为-
(2)若A为三角形的内角,
则0<A<π
又∵f(A)= ,
,
即sin(A- )=
)= ,
,
即cos(A- )=
)=
则sinA=[sin(A- )+
)+ ]=
]=
 +
+
 =
=
则g( )=sinA=
)=sinA=
点评:本题考查的知识点是y=Asin(ωx+φ)中参数的物理意义,函数y=Asin(ωx+φ)的图象变换,三角函数的恒等变换及化简求值,是对正弦型函数的性质及三角函数恒等变换公式的直接考查,熟练掌握基本公式是解答本题的关键.
 个单位后,再把横坐标伸长为原来的2倍(纵坐标不变),得到函数y=f(x)的图象.求出函数的解析式,进而求出其初相.
个单位后,再把横坐标伸长为原来的2倍(纵坐标不变),得到函数y=f(x)的图象.求出函数的解析式,进而求出其初相.(2)根据A为三角形的内角,且f(a)=
 ,我们易根据三角函数同角三角函数关系式,及两角和的正切公式求出A的正弦值,进而得到答案.
,我们易根据三角函数同角三角函数关系式,及两角和的正切公式求出A的正弦值,进而得到答案.解答:解:(1)将函数g(x)=sin2x的图象上各点的横坐标向右平移
 个单位后,
个单位后,再把横坐标伸长为原来的2倍(纵坐标不变),
可以得到函数y=f(x)的图象
∴f(x)=sin(x-
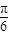 )
)∴函数的初相为-

(2)若A为三角形的内角,
则0<A<π
又∵f(A)=
 ,
,即sin(A-
 )=
)= ,
,即cos(A-
 )=
)=
则sinA=[sin(A-
 )+
)+ ]=
]=
 +
+
 =
=
则g(
 )=sinA=
)=sinA=
点评:本题考查的知识点是y=Asin(ωx+φ)中参数的物理意义,函数y=Asin(ωx+φ)的图象变换,三角函数的恒等变换及化简求值,是对正弦型函数的性质及三角函数恒等变换公式的直接考查,熟练掌握基本公式是解答本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目