题目内容
设关于x的一元二次方程x2+2ax+4-b2=0.(1)如果a∈{0,1,2,3},b∈{0,1,2},求方程有实根的概率;
(2)如果a∈[0,3],b∈[0,2],求方程有实根的概率;
(3)由(2),并结合课本“撒豆子”试验,请你设计一个估算圆周率π的实验,并给出计算公式.
分析:(1)由于a∈{0,1,2,3},b∈{0,1,2},则基本事件总数为3X4=12种,其中满足条件方程有实根,即△≥0,即a2+b2≥4共有8种,代入古典概型公式,即可得到答案.
(2)由于a∈[0,3],b∈[0,2],则基本事件对应的平面区域面积为3X2=6,其中满足条件方程有实根,即△≥0,即a2+b2≥4的平面区域面积为6-π,代入几何概型公式,即可得到答案.
(3)根据(2)中结论,我们易根据频率≈概率的原则,得到当n很大时,比值
,即频率应接近于概率P,于是有P≈
.进而结合(2)的答案,得到结论.
(2)由于a∈[0,3],b∈[0,2],则基本事件对应的平面区域面积为3X2=6,其中满足条件方程有实根,即△≥0,即a2+b2≥4的平面区域面积为6-π,代入几何概型公式,即可得到答案.
(3)根据(2)中结论,我们易根据频率≈概率的原则,得到当n很大时,比值
| n |
| m |
| m |
| n |
解答: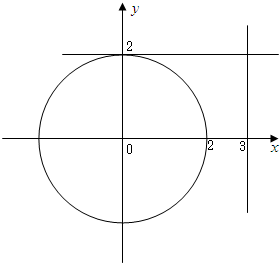 (本小题满分15分)
(本小题满分15分)
解:由方程有实根,则△≥0,得,a2+b2≥4
(1)记“方程有实根”为事件A,则P(A)=
=
.
答:方程有实根的概率为
.…(5分)
(2)记“方程有实根”为事件B,则.
答:方程有实根的概率为1-
.…(10分)
(3)向矩形内撒n颗豆子,其中
落在
圆内的豆子数为m,由(2)
知,豆子落入
圆内的概率P=
,
那么,当n很大时,比值
,即频率应接近于概率P,于是有P≈
.
由此得到π≈
…(15分)
 (本小题满分15分)
(本小题满分15分)解:由方程有实根,则△≥0,得,a2+b2≥4
(1)记“方程有实根”为事件A,则P(A)=
| 8 |
| 12 |
| 2 |
| 3 |
答:方程有实根的概率为
| 2 |
| 3 |
(2)记“方程有实根”为事件B,则.
答:方程有实根的概率为1-
| π |
| 6 |
(3)向矩形内撒n颗豆子,其中
落在
| 1 |
| 4 |
知,豆子落入
| 1 |
| 4 |
| π |
| 6 |
那么,当n很大时,比值
| n |
| m |
| m |
| n |
由此得到π≈
| 6n |
| m |
点评:本题考查的知识点是几何概型与古典概型,根据已知条件计算全部基本事件的个数(几何量)和满足条件的基本事件的个数(几何量)是解答概率问题的关键.(1)(2)中没有结论或假设共扣(2分),(3)中意思表述基本清楚即给全分,也可以直接利用(2)的结论推出公式,公式错误扣(2分).

练习册系列答案
相关题目
 x
x -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
 -2(a-2)x-b
-2(a-2)x-b +16=0.
+16=0. x
x -
- x+1=0(n∈N)有两根α和β,且满足 6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足 6α-2αβ+6β=3. ;
;
 x
x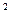 -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.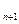 ;
;