题目内容
（本题10分）a，b，c为△ABC的三边，其面积S△ABC＝12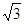
，bc＝48，b-c＝2，求a.
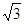，bc＝48，b-c＝2，求a.a2＝b2＋c2-2bccosA＝(b-c)2＋2bc(1-cosA)＝4＋2×48×(1-cosA)
当A＝60°时，a2＝52，a＝2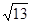
当A＝120°时，a2＝148，a＝2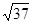
当A＝60°时，a2＝52，a＝2
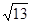当A＝120°时，a2＝148，a＝2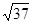由S△ABC＝12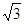，bc＝48,可求出sinA,进而求出cosA,然后再利用
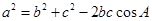求a值即可.
a2＝b2＋c2-2bccosA＝(b-c)2＋2bc(1-cosA)＝4＋2×48×(1-cosA)
当A＝60°时，a2＝52，a＝2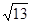 当A＝120°时，a2＝148，a＝2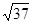
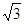，bc＝48,可求出sinA,进而求出cosA,然后再利用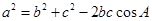求a值即可.a2＝b2＋c2-2bccosA＝(b-c)2＋2bc(1-cosA)＝4＋2×48×(1-cosA)
当A＝60°时，a2＝52，a＝2
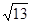当A＝120°时，a2＝148，a＝2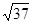
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
中，边
所对的角分别为
，
，则
( )
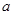=2，b+c=7，cosB=
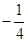，则b=_______。
,则∠C =
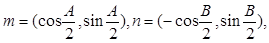且满足
.
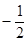求△ABC的面积.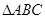 
中，
，则此三角形解的个数为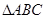
中，如果
，那么角
等于 （ ）
