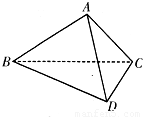
题目内容
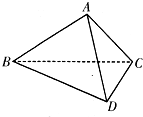 如图所示,在三棱锥A-BCD中,∠BDC为锐角,∠CBD=
如图所示,在三棱锥A-BCD中,∠BDC为锐角,∠CBD=| π |
| 6 |
| 3 |
| 2 |
证明:(1)DC⊥BC;
(2)平面BAC⊥平面ACD;
(3)求点C到平面ABD的距离.
分析:(1)利用正弦定理解△BCD,得sinBDC=
,结合∠BDC为锐角得∠BDC=
,由三角形内角和定理算出∠BCD=
,即得DC⊥BC;
(2)利用勾股定理的逆定理,证出AC⊥CD,结合BC⊥CD,从而证出CD⊥平面BAC,利用线面垂直判定定理即可证出平面BAC⊥平面ACD;
(3)利用题中数据证出△ABC为直角三角形,从而算出S△ABC=2
,由锥体体积公式算出VD-ABC=
.再利用解三角形知识算出△ABD的面积,利用等体积转换加以计算即可算出点C到平面ABD的距离.
| ||
| 2 |
| π |
| 3 |
| π |
| 2 |
(2)利用勾股定理的逆定理,证出AC⊥CD,结合BC⊥CD,从而证出CD⊥平面BAC,利用线面垂直判定定理即可证出平面BAC⊥平面ACD;
(3)利用题中数据证出△ABC为直角三角形,从而算出S△ABC=2
| 2 |
4
| ||
| 3 |
解答:解:(1)在锐角△BCD中,∠CBD=
,BC=2
,CD=2,
∴由正弦定理
=
,得
=
解之得sinBDC=
,结合∠BDC为锐角可得∠BDC=
∴∠BCD=π-∠CBD-∠BDC=
,即DC⊥BC;
(2)在△ACD中,AC=CD=2,AD=2
,
得AC2+CD2=8=AD2,所以AC⊥CD
∵BC⊥CD,AC、BC是平面BAC内的相交直线
∴CD⊥平面BAC
∵CD?平面ACD,∴平面BAC⊥平面ACD;
(3)在△ABC中,AC=2,AB=2
,BC=2
,
∴AC2+AB2=BC2,得AB⊥AC
∴S△ABC=
×AB×AC=2
由(2)知DC⊥平面ABC,故VD-ABC=
×S△ABC×CD=
Rt△BDC中,BD=
=4
在△ABD中,AB=AD=2
,所以AD2+AB2=BD2,故AB⊥AD
故S△ABD=
×AB×AD=4
设点C到平面ABD的距离为h,
可得VC-ABD=VD-ABC,得
S△ABD•h=
,
即
×4×h=
,解之得h=
,即点C到平面ABD的距离
.
| π |
| 6 |
| 3 |

∴由正弦定理
| CD |
| sinCBD |
| BC |
| sinBDC |
| 2 | ||
sin
|
2
| ||
| sinBDC |
解之得sinBDC=
| ||
| 2 |
| π |
| 3 |
∴∠BCD=π-∠CBD-∠BDC=
| π |
| 2 |
(2)在△ACD中,AC=CD=2,AD=2
| 2 |
得AC2+CD2=8=AD2,所以AC⊥CD
∵BC⊥CD,AC、BC是平面BAC内的相交直线
∴CD⊥平面BAC
∵CD?平面ACD,∴平面BAC⊥平面ACD;
(3)在△ABC中,AC=2,AB=2
| 2 |
| 3 |
∴AC2+AB2=BC2,得AB⊥AC
∴S△ABC=
| 1 |
| 2 |
| 2 |
由(2)知DC⊥平面ABC,故VD-ABC=
| 1 |
| 3 |
4
| ||
| 3 |
Rt△BDC中,BD=
| BC2+CD2 |
在△ABD中,AB=AD=2
| 2 |
故S△ABD=
| 1 |
| 2 |
设点C到平面ABD的距离为h,
可得VC-ABD=VD-ABC,得
| 1 |
| 3 |
4
| ||
| 3 |
即
| 1 |
| 3 |
4
| ||
| 3 |
| 2 |
| 2 |
点评:本题给出特殊三棱锥,求证线线垂直、面面垂直,并求锥体的体积,着重考查了解三角形的知识,考查了空间垂直位置关系的证明和锥体体积求法等知识,属于中档题.

练习册系列答案
相关题目
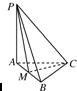 19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.
19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上. 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜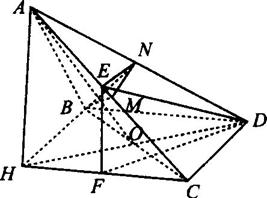
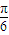 ,BC=
,BC=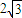 ,CD=AC=2,AB=AD=
,CD=AC=2,AB=AD=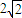 .
.