题目内容
已知函数f(x)=x3+ax2+bx+c,x∈[-2,2]表示的曲线过原点,且在x=±1处的切线斜率均为-1,有以下命题:
①f(x)的解析式为:f(x)=x3-4x,x∈[-2,2]; ②f(x)的极值点有且仅有一个; ③f(x)的最大值与最小值之和等于零,则下列选项正确的是( )
①f(x)的解析式为:f(x)=x3-4x,x∈[-2,2]; ②f(x)的极值点有且仅有一个; ③f(x)的最大值与最小值之和等于零,则下列选项正确的是( )
分析:先求出函数的导数,因为曲线过原点,所以c=0,因为在x=±1处的切线斜率均为-1,所以函数在x=±1处的导数等于-1,再利用导数等于0求极值点,以及函数的最大值与最小值,逐一判断三个命题即可.
解答:解:∵函数f(x)=x3+ax2+bx+c,x∈[-2,2]表示的曲线过原点,∴c=0
对函数f(x)求导,得,f′(x)=3x2+2ax+b,
∵在x=±1处的切线斜率均为-1,∴f′(1)=1,f′(-1)=1,
即,3+2a+b=-1,3-2a+b=-1
解得a=0,b=-4
∴(x)=x3-4x,x∈[-2,2],①正确.
f′(x)=3x2-4,令f′(x)=0,得,x=±
,∴f(x)的极值点有两个,②错误
f(-2)=0,f(-
)=
,f(
)=-
,f(2)=0
∴f(x)的最大值为
,最小值为-
,最大值与最小值之和等于零.③正确.
故选B
对函数f(x)求导,得,f′(x)=3x2+2ax+b,
∵在x=±1处的切线斜率均为-1,∴f′(1)=1,f′(-1)=1,
即,3+2a+b=-1,3-2a+b=-1
解得a=0,b=-4
∴(x)=x3-4x,x∈[-2,2],①正确.
f′(x)=3x2-4,令f′(x)=0,得,x=±
2
| ||
| 3 |
f(-2)=0,f(-
2
| ||
| 3 |
16
| ||
| 6 |
2
| ||
| 3 |
16
| ||
| 6 |
∴f(x)的最大值为
16
| ||
| 6 |
16
| ||
| 6 |
故选B
点评:本题考查了应用导数求函数的极值点,最大值与最小值,属于导数的应用的常规题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
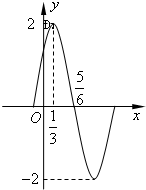 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|