��Ŀ����
��2013•�ع�һģ����f��x��������I���ж��壬����?x1��x2��I������f(
)��
�����f��x��������I����������������?x1��x2��I������f(
)��
�����f��x��������I�������������������ĸ��жϣ�
����f��x��������I��������������-f��x��������I������������
����f��x����g��x����������I��������������f��x��+g��x��������I������������
����f��x��������I��������������f��x����0����
������I������������
����f��x��������I������������?x1��x2��x3��x4��I������f��
����
������ȷ�Ľ��۸����ǣ�������
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
����f��x��������I��������������-f��x��������I������������
����f��x����g��x����������I��������������f��x��+g��x��������I������������
����f��x��������I��������������f��x����0����
| 1 |
| f(x) |
����f��x��������I������������?x1��x2��x3��x4��I������f��
| x1+x2+x3+x4 |
| 4 |
| f(x1)+f(x2)+f(x3)+f(x4) |
| 4 |
������ȷ�Ľ��۸����ǣ�������
���������ڢ٢ڢ�ֱ�����ú����ǡ��������Ķ��壬ͨ��������֤�����ɣ����ڢ����þٷ����ķ������ͼ���ɽ����жϣ�
����⣺����f��x��������I���������������?x1��x2��I������f(
)��
��
��-f(
)��
��
��-f��x��������I��������������ȷ��
����f��x����g��x����������I���������������?x1��x2��I������f(
)��
��
g(
)��
����ʽ��ӵ�f(
)+g(
)��
+
��f��x��+g��x��������I��������������ȷ��
����f��x��������I��������������f��x����0����
��һ��������I������������
��f��x��=ex��
=(
)x����ͼ��
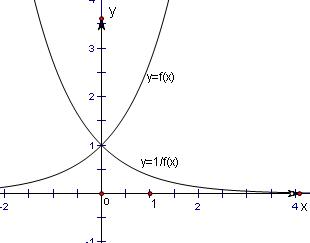
���Ƕ��������������ʴ���
����f��x��������I������������
?x1��x2��x3��x4��I������f��
��=f��
����
��
������ȷ��
������ȷ�Ľ��۸�����3��
��ѡC��
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
��-f(
| x1+x2 |
| 2 |
| -f(x1)-f(x2) |
| 2 |
��-f��x��������I��������������ȷ��
����f��x����g��x����������I���������������?x1��x2��I������f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
g(
| x1+x2 |
| 2 |
| g(x1)+g(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| g(x1)+g(x2) |
| 2 |
��f��x��+g��x��������I��������������ȷ��
����f��x��������I��������������f��x����0����
| 1 |
| f(x) |
��f��x��=ex��
| 1 |
| f(x) |
| 1 |
| e |

���Ƕ��������������ʴ���
����f��x��������I������������
?x1��x2��x3��x4��I������f��
| x1+x2+x3+x4 |
| 4 |
| ||||
| 2 |
f(
| ||||
| 2 |
��
| f(x1)+f(x2)+f(x3)+f(x4) |
| 4 |
������ȷ�Ľ��۸�����3��
��ѡC��
���������⿼�����������ж���Ӧ���Լ�������֤������IJ��裬�¶����Ӧ�ã���������������������������

��ϰ��ϵ�д�
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
�����Ŀ
 ��2013•�ع�һģ����ͼ������P-ABC�У�PB�͵���ABC��B����BCA=90�㣬PB=CA=2����E��PC���е㣮
��2013•�ع�һģ����ͼ������P-ABC�У�PB�͵���ABC��B����BCA=90�㣬PB=CA=2����E��PC���е㣮