题目内容
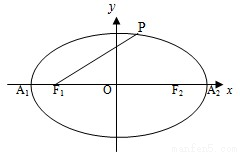
如图,椭圆C: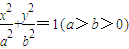 ,A1、A2为椭圆C的左、右顶点.
,A1、A2为椭圆C的左、右顶点.(Ⅰ)设F1为椭圆C的左焦点,证明:当且仅当椭圆C上的点P在椭圆的左、右顶点时|PF1|取得最小值与最大值;
(Ⅱ)若椭圆C上的点到焦点距离的最大值为3,最小值为1.求椭圆C的标准方程;
(Ⅲ)若直线l:y=kx+m与(Ⅱ)中所述椭圆C相交于A,B两点(A,B不是左右顶点),且满足AA2⊥BA2,求证:直线l过定点,并求出该定点的坐标.
【答案】分析:(I)设点P的坐标(x,y),再构造函数f(x)=|PF1|2,代入两点间的距离公式并进行化简,利用二次函数的性质和x的范围,求出函数的最值以及对应的x的取值,即得到证明;
(Ⅱ)由已知与(Ⅰ)得:a+c=3,a-c=1,解得a=2,c=1,再由b2=a2-c2求出b,进而求出椭圆的标准方程;
(Ⅲ)假设存在满足条件的直线,再设A(x1,y1),B(x2,y2),联立直线方程和椭圆方程进行整理,化简出一个二次方程,再由题意和韦达定理列出方程组,根据题意得 ,代入后得列出关于m的方程,进行化简、求解,注意对应题意进行验证.
,代入后得列出关于m的方程,进行化简、求解,注意对应题意进行验证.
解答:解:(Ⅰ)设p(x,y),则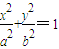 ,且F1(-c,0),
,且F1(-c,0),
设f(x)=|PF1|2,则f(x)=(x+c)2+y2=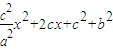 ,
,
∴对称轴方程 ,由题意知,
,由题意知,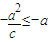 恒成立,
恒成立,
∴f(x)在区间[-a,a]上单调递增,
∴当x取-a、a时,函数分别取到最小值与最大值,
∴当且仅当椭圆C上的点P在椭圆的左、右顶点时|PF1|取得最小值与最大值;
(Ⅱ)由已知与(Ⅰ)得:a+c=3,a-c=1,解得a=2,c=1,∴b2=a2-c2=3,
∴椭圆的标准方程为 .
.
(Ⅲ)假设存在满足条件的直线l,设A(x1,y1),B(x2,y2),
联立 得,(3+4k2)x2+8mkx+4(m2-3)=0,则
得,(3+4k2)x2+8mkx+4(m2-3)=0,则
又∵ ,
,
∵椭圆的右顶点为A2(2,0),AA2⊥BA2,∴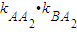 =-1,
=-1,
即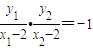 ,∴y1y2+x1x2-2(x1+x2)+4=0,
,∴y1y2+x1x2-2(x1+x2)+4=0,
∴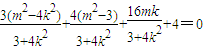 ,
,
化简得,7m2+16mk+4k2=0,
解得,m1=-2k,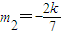 ,且均满足3+4k2-m2>0,
,且均满足3+4k2-m2>0,
当m1=-2k时,l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
当 时,l的方程为
时,l的方程为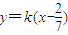 ,直线过定点
,直线过定点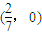 .
.
所以,直线l过定点,定点坐标为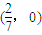 .
.
点评:本题考查椭圆的方程和椭圆简单的几何性质,以及直线与椭圆的位置关系,同时也考查了利用构造函数的方法处理最值问题,主要利用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力,最后对应题意进行验证这是易错的地方.
(Ⅱ)由已知与(Ⅰ)得:a+c=3,a-c=1,解得a=2,c=1,再由b2=a2-c2求出b,进而求出椭圆的标准方程;
(Ⅲ)假设存在满足条件的直线,再设A(x1,y1),B(x2,y2),联立直线方程和椭圆方程进行整理,化简出一个二次方程,再由题意和韦达定理列出方程组,根据题意得
 ,代入后得列出关于m的方程,进行化简、求解,注意对应题意进行验证.
,代入后得列出关于m的方程,进行化简、求解,注意对应题意进行验证.解答:解:(Ⅰ)设p(x,y),则
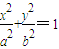 ,且F1(-c,0),
,且F1(-c,0),设f(x)=|PF1|2,则f(x)=(x+c)2+y2=
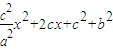 ,
,∴对称轴方程
 ,由题意知,
,由题意知,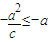 恒成立,
恒成立,∴f(x)在区间[-a,a]上单调递增,
∴当x取-a、a时,函数分别取到最小值与最大值,
∴当且仅当椭圆C上的点P在椭圆的左、右顶点时|PF1|取得最小值与最大值;
(Ⅱ)由已知与(Ⅰ)得:a+c=3,a-c=1,解得a=2,c=1,∴b2=a2-c2=3,
∴椭圆的标准方程为
 .
.(Ⅲ)假设存在满足条件的直线l,设A(x1,y1),B(x2,y2),
联立
 得,(3+4k2)x2+8mkx+4(m2-3)=0,则
得,(3+4k2)x2+8mkx+4(m2-3)=0,则
又∵
 ,
,∵椭圆的右顶点为A2(2,0),AA2⊥BA2,∴
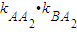 =-1,
=-1,即
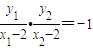 ,∴y1y2+x1x2-2(x1+x2)+4=0,
,∴y1y2+x1x2-2(x1+x2)+4=0,∴
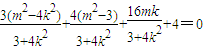 ,
,化简得,7m2+16mk+4k2=0,
解得,m1=-2k,
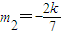 ,且均满足3+4k2-m2>0,
,且均满足3+4k2-m2>0,当m1=-2k时,l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
当
 时,l的方程为
时,l的方程为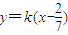 ,直线过定点
,直线过定点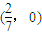 .
.所以,直线l过定点,定点坐标为
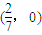 .
.点评:本题考查椭圆的方程和椭圆简单的几何性质,以及直线与椭圆的位置关系,同时也考查了利用构造函数的方法处理最值问题,主要利用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力,最后对应题意进行验证这是易错的地方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
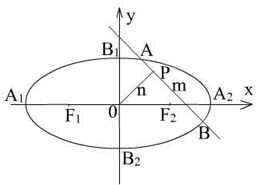 如图,椭圆C:
如图,椭圆C: (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 如图,椭圆
如图,椭圆 ,A1、A2为椭圆C的左、右顶点.
,A1、A2为椭圆C的左、右顶点.